题目内容
15. 如图,已知∠ACB=∠ABD=90°,CA=CB=6,∠DAB=30°,求以BD为直径的圆的面积.
如图,已知∠ACB=∠ABD=90°,CA=CB=6,∠DAB=30°,求以BD为直径的圆的面积.
分析 首先利用勾股定理可得AB的长,在直角三角形ABD中,由锐角三角函数定义可得BD的长,由圆的面积公式可得结果.
解答 解:∵∠ACB=∠ABD=90°,CA=CB=6,
∴AB=$\sqrt{{AC}^{2}{+BC}^{2}}$=$\sqrt{{6}^{2}{+6}^{2}}$=6$\sqrt{2}$,
∵∠DAB=30°,
∴BD=AB•tan30°=6$\sqrt{2}$×$\frac{\sqrt{3}}{3}$=2$\sqrt{6}$,
∴以BD为直径的圆的面积为:${(\frac{2\sqrt{6}}{2})}^{2}$×π=6π.
点评 本题主要考查了锐角三角函数的定义和勾股定理,利用勾股定理和锐角三角函数的定义求得BD的长是解答此题的关键.

练习册系列答案
相关题目
10.把一段为40cm的铁丝穹成一个长方形,设长方形的一边长为a cm.
(1)写出表示这个长方形面积的代数式;
(2)完成下表
(3)你认为当a取何值时,长方形的面积最大?这时,长方形的形状是什么样的?
(1)写出表示这个长方形面积的代数式;
(2)完成下表
| 长方形一边的长a/cm | 6 | 8 | 10 | 12 | 14 | 16 |
| 长方形的面积/cm2 | 84 | 96 | 100 | 96 | 84 | 64 |
 如图所示,CD为⊙O的弦,P为劣弧$\widehat{CD}$上的任意一点(不与点C,D重合),AB为⊙O的直径,∠APC=∠APD,试判断CD与AB的位置关系,并说明理由.
如图所示,CD为⊙O的弦,P为劣弧$\widehat{CD}$上的任意一点(不与点C,D重合),AB为⊙O的直径,∠APC=∠APD,试判断CD与AB的位置关系,并说明理由.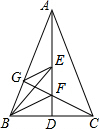 如图,在△ABC中,AD⊥BC于D,AB=AC,BE、BF将∠ABC三等分交AD于E、F,CF延长线交AB于G,求证:GE∥BF.
如图,在△ABC中,AD⊥BC于D,AB=AC,BE、BF将∠ABC三等分交AD于E、F,CF延长线交AB于G,求证:GE∥BF. 如图,在矩形纸片ABCD中,AB=14,BC=8,点E为边BC上一点,且BE=5,将纸片沿过点E的一条直线l翻折,使点B落在直线CD上,若l与矩形的边的另一个交点为F,则EF的长为5$\sqrt{5}$.
如图,在矩形纸片ABCD中,AB=14,BC=8,点E为边BC上一点,且BE=5,将纸片沿过点E的一条直线l翻折,使点B落在直线CD上,若l与矩形的边的另一个交点为F,则EF的长为5$\sqrt{5}$.