题目内容
10. 将下列推理过程中的依据补充完整.
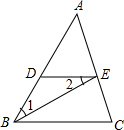
将下列推理过程中的依据补充完整.已知:如图:∠1=∠2,且BE平分∠ABC,求证:∠AED=∠C.
证明:∵BE平分∠ABC(已知),
∴∠1=∠EBC(角平分线的定义)
又∵∠1=∠2(已知)
∴∠2=∠EBC(等量代换)
∴DE∥BC(内错角相等,两直线平行)
∴∠AED=∠C(两直线平行,同位角相等)
分析 先根据等量代换,得出∠2=∠EBC,再根据平行线的判定,得出DE∥BC,最后根据平行线的性质,得出∠AED=∠C.
解答 证明:∵BE平分∠ABC(已知),
∴∠1=∠EBC(角平分线的定义),
又∵∠1=∠2(已知),
∴∠2=∠EBC(等量代换),
∴DE∥BC(内错角相等,两直线平行),
∴∠AED=∠C(两直线平行,同位角相等).
故答案为:已知,角平分线的定义,已知,等量代换,内错角相等,两直线平行,两直线平行,同位角相等
点评 本题主要考查了平行线的性质与判定,平行线的判定是由角的数量关系判断两直线的位置关系;平行线的性质是由平行关系来寻找角的数量关系.

练习册系列答案
相关题目
20. 如图,在梯形ABCD中,AD∥BC,连接AC、BD,则图中面积相等的三角形共有( )
如图,在梯形ABCD中,AD∥BC,连接AC、BD,则图中面积相等的三角形共有( )
 如图,在梯形ABCD中,AD∥BC,连接AC、BD,则图中面积相等的三角形共有( )
如图,在梯形ABCD中,AD∥BC,连接AC、BD,则图中面积相等的三角形共有( )| A. | 4对 | B. | 1对 | C. | 2对 | D. | 3对 |
15.三角形的两边长分别为3和6,第三边的长是方程x2-6x+8=0的一个根,则这个三角形的周长是( )
| A. | 9 | B. | 11 | C. | 13 | D. | 11或13 |
2. 如图所示,Rt△ABC中,∠C=90°,AC=6,BC=8,两等圆圆A,圆B外切,那么图中两个扇形(即阴影部分)的面积之和为( )
如图所示,Rt△ABC中,∠C=90°,AC=6,BC=8,两等圆圆A,圆B外切,那么图中两个扇形(即阴影部分)的面积之和为( )
 如图所示,Rt△ABC中,∠C=90°,AC=6,BC=8,两等圆圆A,圆B外切,那么图中两个扇形(即阴影部分)的面积之和为( )
如图所示,Rt△ABC中,∠C=90°,AC=6,BC=8,两等圆圆A,圆B外切,那么图中两个扇形(即阴影部分)的面积之和为( )| A. | $\frac{25}{4}$π | B. | $\frac{25}{8}π$ | C. | $\frac{25}{16}π$ | D. | $\frac{25}{32}π$ |
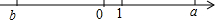 数轴上有b,0,1,a的四个数,如图所示,已知|a|=|b|,化简:|b+1|+|$\frac{a}{b}$|-|a+b|.
数轴上有b,0,1,a的四个数,如图所示,已知|a|=|b|,化简:|b+1|+|$\frac{a}{b}$|-|a+b|.