题目内容
2. 如图所示,Rt△ABC中,∠C=90°,AC=6,BC=8,两等圆圆A,圆B外切,那么图中两个扇形(即阴影部分)的面积之和为( )
如图所示,Rt△ABC中,∠C=90°,AC=6,BC=8,两等圆圆A,圆B外切,那么图中两个扇形(即阴影部分)的面积之和为( )| A. | $\frac{25}{4}$π | B. | $\frac{25}{8}π$ | C. | $\frac{25}{16}π$ | D. | $\frac{25}{32}π$ |
分析 首先计算出AB长,由等圆⊙B,⊙C外切,即可求得⊙B,⊙C的半径为5,又由△ACB中,∠C=90°,即可得∠B+∠A=90°,然后根据扇形的面积的求解方法求解即可求得答案.
解答 解:∵∠C=90°,AC=6,BC=8,
∴AB=$\sqrt{{6}^{2}+{8}^{2}}$=10,
∵等圆⊙B,⊙A外切,
∴⊙B,⊙C的半径为5,
∵△ACB中,∠C=90°,
∴∠B+∠A=90°,
∴两圆中阴影扇形的面积之和为:$\frac{∠B×π×{5}^{2}}{360°}$+$\frac{∠C×π×{5}^{2}}{360°}$=$\frac{1}{360°}$π×(∠B+∠C)×25=$\frac{25}{4}$π.
故选:A.
点评 此题考查了相切两圆的性质、扇形的面积以及直角三角形的性质.此题难度不大,注意掌握数形结合思想与整体思想的应用.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
 如图,已知正方形A1B1C1D1的面积为1,把它的各边延长一倍得到新的正方形A2B2C2D2,再将正方形A2B2C2D2各边长延长一倍得到正方形A3B3C3D3,以此下去…,则正方形A9B9C9D9的周长是2500.
如图,已知正方形A1B1C1D1的面积为1,把它的各边延长一倍得到新的正方形A2B2C2D2,再将正方形A2B2C2D2各边长延长一倍得到正方形A3B3C3D3,以此下去…,则正方形A9B9C9D9的周长是2500.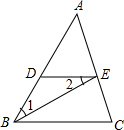 将下列推理过程中的依据补充完整.
将下列推理过程中的依据补充完整.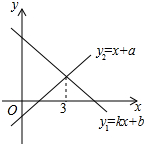 一次函数y1=kx+b与y2=x+a的图象如图所示,则下列结论:①k>0;②a>0;③当x<3时,y1<y2中,正确的个数是( )
一次函数y1=kx+b与y2=x+a的图象如图所示,则下列结论:①k>0;②a>0;③当x<3时,y1<y2中,正确的个数是( ) △ABC为锐角三角形,BD、CE为高,求证:△ADE∽△ABC.
△ABC为锐角三角形,BD、CE为高,求证:△ADE∽△ABC.