题目内容
4.如果不等式组$\left\{\begin{array}{l}{x>3}\\{x<m}\end{array}\right.$无解,那么m的取值范围是m≤3.分析 由不等式组无解,利用不等式组取解集的方法确定出m的范围即可.
解答 解:∵不等式组$\left\{\begin{array}{l}{x>3}\\{x<m}\end{array}\right.$无解,
∴m≤3,
故答案为:m≤3
点评 此题考查了不等式的解集,熟练掌握不等式组取解集的方法是解本题的关键.

练习册系列答案
相关题目
14.能够判定一个四边形是菱形的条件是( )
| A. | 对角线互相垂直平分 | B. | 对角线互相平分且相等 | ||
| C. | 对角线相等且互相垂直 | D. | 对角线互相垂直 |
15.下列多项式中,不能用平方差公式分解的是( )
| A. | -m4-n4 | B. | -16x2+y2 | C. | 1.96-x2 | D. | $\frac{1}{9}$a2-$\frac{1}{4}$b2 |
19.已知矩形的较短边长为6,对角线相交成60°角,则这个矩形的较长边的长是( )
| A. | 3$\sqrt{6}$ | B. | 6$\sqrt{3}$ | C. | 9 | D. | 12 |
13.若不等式组$\left\{\begin{array}{l}{x+a≥0}\\{1-2x>x-2}\end{array}\right.$有三个整数解,则实数a的取值范围是( )
| A. | 2≤a≤3 | B. | 2<a≤3 | C. | 2≤a<3 | D. | 2<a<3 |
14.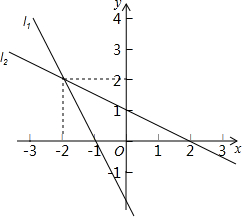 如图,直线l1的解析式为y1=k1x+b1,直线l2的解析式为y2=k2x+b2,则不等式k1x+b1>k2x+b2的解集是( )
如图,直线l1的解析式为y1=k1x+b1,直线l2的解析式为y2=k2x+b2,则不等式k1x+b1>k2x+b2的解集是( )
 如图,直线l1的解析式为y1=k1x+b1,直线l2的解析式为y2=k2x+b2,则不等式k1x+b1>k2x+b2的解集是( )
如图,直线l1的解析式为y1=k1x+b1,直线l2的解析式为y2=k2x+b2,则不等式k1x+b1>k2x+b2的解集是( )| A. | x>2 | B. | x<2 | C. | x>-2 | D. | x<-2 |
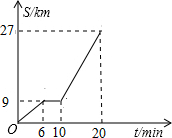 如图所示是鼎龙高速路口开往宁都方向的某汽车行驶的路程s(km)与时间t(分钟)的函数关系图,观察图中所提供的信息,解答下列问题:
如图所示是鼎龙高速路口开往宁都方向的某汽车行驶的路程s(km)与时间t(分钟)的函数关系图,观察图中所提供的信息,解答下列问题: 如图,在平行四边形ABCD中,AB=$\sqrt{29}$,AD=4,将平行四边形ABCD沿AE翻折后,点B恰好与点C重合,则折痕AE的长为( )
如图,在平行四边形ABCD中,AB=$\sqrt{29}$,AD=4,将平行四边形ABCD沿AE翻折后,点B恰好与点C重合,则折痕AE的长为( )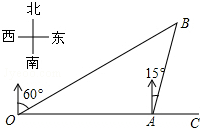 如图,港口A在观测站O的正东方向相距4km,某船从A出发,沿北偏东15°方向航行5分钟后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,求该船航行的速度(精确到整数位).参考数值:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732.
如图,港口A在观测站O的正东方向相距4km,某船从A出发,沿北偏东15°方向航行5分钟后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,求该船航行的速度(精确到整数位).参考数值:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732.