题目内容
19.已知矩形的较短边长为6,对角线相交成60°角,则这个矩形的较长边的长是( )| A. | 3$\sqrt{6}$ | B. | 6$\sqrt{3}$ | C. | 9 | D. | 12 |
分析 根据矩形对角线相等且互相平分性质和题中条件易得△AOB为等边三角形,即可得到矩形对角线一半长,进而求解即可.
解答 解:如图:AB=6,∠AOB=60°,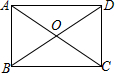
∵四边形是矩形,AC,BD是对角线,
∴OA=OB=OD=OC=$\frac{1}{2}$BD=$\frac{1}{2}$AC,
在△AOB中,OA=OB,∠AOB=60°,
∴OA=OB=AB=6,BD=2OB=12,
∴BC=$\sqrt{1{2}^{2}-{6}^{2}}$=6$\sqrt{3}$,
故选B.
点评 此题考查矩形的性质,矩形的两对角线所夹的角为60°,那么对角线的一边和两条对角线的一半组成等边三角形.本题比较简单,根据矩形的性质解答即可.

练习册系列答案
相关题目
9.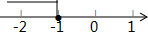 关于x的不等式2x+a≤-3的解集如图所示,则a的取值是( )
关于x的不等式2x+a≤-3的解集如图所示,则a的取值是( )
 关于x的不等式2x+a≤-3的解集如图所示,则a的取值是( )
关于x的不等式2x+a≤-3的解集如图所示,则a的取值是( )| A. | 0 | B. | -1 | C. | -2 | D. | -3 |
14.下列图形不一定是轴对称图形的是( )
| A. | 直角三角形 | B. | 钝角 | C. | 线段 | D. | 圆 |
11. 如图,点O是平行四边形ABCD的对角线的交点,则图中全等三角形共有( )
如图,点O是平行四边形ABCD的对角线的交点,则图中全等三角形共有( )
 如图,点O是平行四边形ABCD的对角线的交点,则图中全等三角形共有( )
如图,点O是平行四边形ABCD的对角线的交点,则图中全等三角形共有( )| A. | 4对 | B. | 3对 | C. | 2对 | D. | 1对 |
8. 如图,?ABCD中,AB=4,BC=3,∠DCB=30°,动点E从B点出发,沿B-C-D-A运动至A点停止,设运动的路程为x,△ABE的面积为y,则y与x的函数图象用图象表示正确的是( )
如图,?ABCD中,AB=4,BC=3,∠DCB=30°,动点E从B点出发,沿B-C-D-A运动至A点停止,设运动的路程为x,△ABE的面积为y,则y与x的函数图象用图象表示正确的是( )
 如图,?ABCD中,AB=4,BC=3,∠DCB=30°,动点E从B点出发,沿B-C-D-A运动至A点停止,设运动的路程为x,△ABE的面积为y,则y与x的函数图象用图象表示正确的是( )
如图,?ABCD中,AB=4,BC=3,∠DCB=30°,动点E从B点出发,沿B-C-D-A运动至A点停止,设运动的路程为x,△ABE的面积为y,则y与x的函数图象用图象表示正确的是( )| A. | 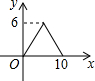 | B. |  | C. | 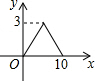 | D. | 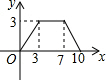 |
9.下列各式中正确的是( )
| A. | $\sqrt{25}$=±5 | B. | ±$\sqrt{36}$=±6 | C. | $\sqrt{-100}$=10 | D. | $\sqrt{(-3)^{2}}$=-3 |