题目内容
14.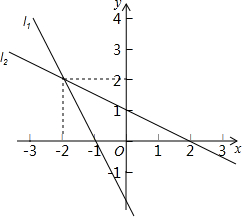 如图,直线l1的解析式为y1=k1x+b1,直线l2的解析式为y2=k2x+b2,则不等式k1x+b1>k2x+b2的解集是( )
如图,直线l1的解析式为y1=k1x+b1,直线l2的解析式为y2=k2x+b2,则不等式k1x+b1>k2x+b2的解集是( )| A. | x>2 | B. | x<2 | C. | x>-2 | D. | x<-2 |
分析 由图象可以知道,当x=-2时,两个函数的函数值是相等的,再根据函数的增减性可以判断出不等式k1x+b1>k2x+b2解集.
解答 解:两个条直线的交点坐标为(-2,2),且当x<-2时,直线l1在直线l2的上方,
故不等k1x+b1>k2x+b2的解集为x<-2.
故选D.
点评 此题主要考查了一次函数的图象解一元一次不等式,两个图象的“交点”是两个函数值大小关系的“分界点”,在“分界点”处函数值的大小发生了改变.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
5.?ABCD中,∠A=30°,AB边上的高为6,则BC的长为( )
| A. | 12 | B. | 6 | C. | 6$\sqrt{2}$ | D. | 6$\sqrt{3}$ |
9.下列各式中正确的是( )
| A. | $\sqrt{25}$=±5 | B. | ±$\sqrt{36}$=±6 | C. | $\sqrt{-100}$=10 | D. | $\sqrt{(-3)^{2}}$=-3 |
19. 如图,下列条件能判定AD∥BC的是( )
如图,下列条件能判定AD∥BC的是( )
 如图,下列条件能判定AD∥BC的是( )
如图,下列条件能判定AD∥BC的是( )| A. | ∠C=∠CBE | B. | ∠C+∠ABC=180° | C. | ∠FDC=∠C | D. | ∠FDC=∠A |
6.若代数式$\frac{1}{\sqrt{x-1}}$在实数范围内有意义,则x的取值范围是( )
| A. | x>1 | B. | x≥1 | C. | x≠1 | D. | x>0且x≠1 |
4.用下列多边形不能单独铺满地面的是( )
| A. | 正三角形 | B. | 正四边形 | C. | 正六边形 | D. | 正八边形 |
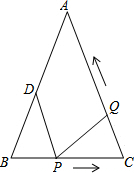 如图,已知△ABC中,AB=AC=10cm,BC=8cm,D为AB的中点,点P在线段BC上由B点出发向C点运动,同时点Q在线段CA上由C点出发向A点运动.设运动时间为ts.
如图,已知△ABC中,AB=AC=10cm,BC=8cm,D为AB的中点,点P在线段BC上由B点出发向C点运动,同时点Q在线段CA上由C点出发向A点运动.设运动时间为ts.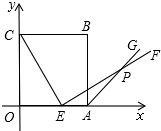 如图,边长为5的正方形OABC的顶点O在坐标原点处,点A、C分别在x轴、y轴的正半轴上,点E是OA边上的点(不与点A重合),EF⊥CE,且与正方形外角平分线AG交于点P.
如图,边长为5的正方形OABC的顶点O在坐标原点处,点A、C分别在x轴、y轴的正半轴上,点E是OA边上的点(不与点A重合),EF⊥CE,且与正方形外角平分线AG交于点P.