题目内容
16.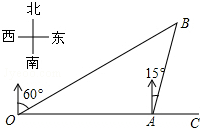 如图,港口A在观测站O的正东方向相距4km,某船从A出发,沿北偏东15°方向航行5分钟后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,求该船航行的速度(精确到整数位).参考数值:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732.
如图,港口A在观测站O的正东方向相距4km,某船从A出发,沿北偏东15°方向航行5分钟后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,求该船航行的速度(精确到整数位).参考数值:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732.
分析 过点A作AD⊥OB于D.先解Rt△AOD,得出AD的长度,再由△ABD是等腰直角三角形,得出BD=AD=2km,则易得AB、AD的长度;最后结合速度=路程÷时间解答问题.
解答 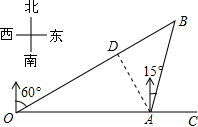 解:如图,过点A作AD⊥OB于D.
解:如图,过点A作AD⊥OB于D.
在Rt△AOD中,∵∠ADO=90°,∠AOD=30°,OA=4km,
∴AD=$\frac{1}{2}$OA=2km.
在Rt△ABD中,∵∠ADB=90°,∠B=∠CAB-∠AOB=75°-30°=45°,
∴BD=AD=2km,
∴AB=$\sqrt{2}$AD=2$\sqrt{2}$km.
即该船航行的距离(即AB的长)为2$\sqrt{2}$km.
∴2$\sqrt{2}$÷$\frac{1}{12}$=24×1.414÷5≈34(km/h).
答:该船航行的速度约为34km/h.
点评 本题考查了解直角三角形的应用-方向角问题,难度适中,作出辅助线构造直角三角形是解题的关键.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
6.下列命题中,是真命题的是( )
①两条直线被第三条直线所截,同位角相等;
②在同一平面内,垂直于同一直线的两条直线互相平行
③三角形的三条高中,必有一条在三角形的内部
④$\sqrt{-2}$是一个负数.
①两条直线被第三条直线所截,同位角相等;
②在同一平面内,垂直于同一直线的两条直线互相平行
③三角形的三条高中,必有一条在三角形的内部
④$\sqrt{-2}$是一个负数.
| A. | ①② | B. | ②③ | C. | ①③ | D. | ③④ |
11. 如图,点O是平行四边形ABCD的对角线的交点,则图中全等三角形共有( )
如图,点O是平行四边形ABCD的对角线的交点,则图中全等三角形共有( )
 如图,点O是平行四边形ABCD的对角线的交点,则图中全等三角形共有( )
如图,点O是平行四边形ABCD的对角线的交点,则图中全等三角形共有( )| A. | 4对 | B. | 3对 | C. | 2对 | D. | 1对 |
8. 如图,?ABCD中,AB=4,BC=3,∠DCB=30°,动点E从B点出发,沿B-C-D-A运动至A点停止,设运动的路程为x,△ABE的面积为y,则y与x的函数图象用图象表示正确的是( )
如图,?ABCD中,AB=4,BC=3,∠DCB=30°,动点E从B点出发,沿B-C-D-A运动至A点停止,设运动的路程为x,△ABE的面积为y,则y与x的函数图象用图象表示正确的是( )
 如图,?ABCD中,AB=4,BC=3,∠DCB=30°,动点E从B点出发,沿B-C-D-A运动至A点停止,设运动的路程为x,△ABE的面积为y,则y与x的函数图象用图象表示正确的是( )
如图,?ABCD中,AB=4,BC=3,∠DCB=30°,动点E从B点出发,沿B-C-D-A运动至A点停止,设运动的路程为x,△ABE的面积为y,则y与x的函数图象用图象表示正确的是( )| A. | 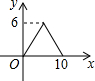 | B. |  | C. | 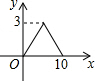 | D. | 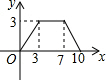 |
5.?ABCD中,∠A=30°,AB边上的高为6,则BC的长为( )
| A. | 12 | B. | 6 | C. | 6$\sqrt{2}$ | D. | 6$\sqrt{3}$ |
6.若代数式$\frac{1}{\sqrt{x-1}}$在实数范围内有意义,则x的取值范围是( )
| A. | x>1 | B. | x≥1 | C. | x≠1 | D. | x>0且x≠1 |