题目内容
13．若不等式组$\left\{\begin{array}{l}{x+a≥0}\\{1-2x＞x-2}\end{array}\right.$有三个整数解，则实数a的取值范围是（ ）| A． | 2≤a≤3 | B． | 2＜a≤3 | C． | 2≤a＜3 | D． | 2＜a＜3 |
分析 此题需要首先解不等式，根据解的情况确定a的取值范围．特别是要注意不等号中等号的取舍．
解答 解：解不等式x+a≥0得：x≥-a，
解不等式1-2x＞x-2得：x＜1，
∵此不等式组有3个整数解，
∴这3个整数解为-2，-1，0，
∴a的取值范围是-3＜a≤-2．
故选：C．
点评 此题考查了一元一次不等式组的解法．解题中要注意分析不等式组的解集的确定．
练习册系列答案
相关题目
8．
如图，?ABCD中，AB=4，BC=3，∠DCB=30°，动点E从B点出发，沿B-C-D-A运动至A点停止，设运动的路程为x，△ABE的面积为y，则y与x的函数图象用图象表示正确的是（ ）
如图，?ABCD中，AB=4，BC=3，∠DCB=30°，动点E从B点出发，沿B-C-D-A运动至A点停止，设运动的路程为x，△ABE的面积为y，则y与x的函数图象用图象表示正确的是（ ）| A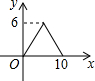． |  | B． |  | C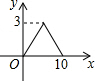． |  | D． |  |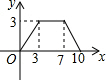
18．直线y=-$\frac{2}{3}$x+$\frac{1}{2}$不经过的象限是（ ）
| A． | 一 | B． | 二 | C． | 三 | D． | 四 |
5．?ABCD中，∠A=30°，AB边上的高为6，则BC的长为（ ）
| A． | 12 | B． | 6 | C． | 6$\sqrt{2}$ | D． | 6$\sqrt{3}$ |
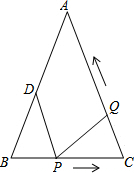如图，已知△ABC中，AB=AC=10cm，BC=8cm，D为AB的中点，点P在线段BC上由B点出发向C点运动，同时点Q在线段CA上由C点出发向A点运动．设运动时间为ts．
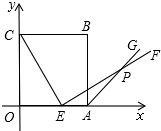如图，边长为5的正方形OABC的顶点O在坐标原点处，点A、C分别在x轴、y轴的正半轴上，点E是OA边上的点（不与点A重合），EF⊥CE，且与正方形外角平分线AG交于点P．