题目内容
14．能够判定一个四边形是菱形的条件是（ ）| A． | 对角线互相垂直平分 | B． | 对角线互相平分且相等 | ||
| C． | 对角线相等且互相垂直 | D． | 对角线互相垂直 |
分析 根据菱形的判定方法一一判断即可解决问题．
解答 解：A、正确．因为四边形的对角线互相平分，所以这个四边形是平行四边形，又因为对角线互相垂直，所以四边形是菱形，故正确．
B、错误．因为对角线互相平分且相等，所以四边形是矩形，故错误．
C、错误．对角线相等且垂直，无法判断四边形是菱形，故错误．
D、错误．对角线互相垂直，无法判断四边形是菱形，故错误．
故选A
点评 本题考查菱形的判定、平行四边形的判定．矩形的判断等知识，解题的关键是记住这些知识灵活解决问题，所以中考常考题型．
练习册系列答案
相关题目
9．
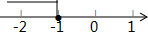关于x的不等式2x+a≤-3的解集如图所示，则a的取值是（ ）
关于x的不等式2x+a≤-3的解集如图所示，则a的取值是（ ）| A． | 0 | B． | -1 | C． | -2 | D． | -3 |
19．
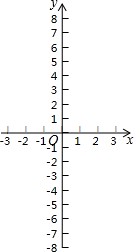六个函数分别是①y=x；②y=-x+1；③y=x2；④y=-x2+2x-1；⑤y=x3；⑥y=-x3+1．
（1）其中一次函数是①，②，二次函数是③，④，则⑤，⑥的函数可以定义为三次函数；
（2）我们可以借鉴以前研究函数的经验，先探索函数y=x3的图象和性质；
①填写下表，画出函数的图象；
②观察图象，写出该函数两条不同类型的性质；
（3）若点A（a，b）（a＞0）是函数y=x3图象上一点，点A关于y轴的对称点为点B，点A关于原点O的对称点为点C，若顺次连接A，B，C，则△ABC的形状为直角三角形；
（4）函数y=-x3+1的图象关于点（0，1）成中心对称图形．
六个函数分别是①y=x；②y=-x+1；③y=x2；④y=-x2+2x-1；⑤y=x3；⑥y=-x3+1．（1）其中一次函数是①，②，二次函数是③，④，则⑤，⑥的函数可以定义为三次函数；
（2）我们可以借鉴以前研究函数的经验，先探索函数y=x3的图象和性质；
①填写下表，画出函数的图象；
②观察图象，写出该函数两条不同类型的性质；
| x | … | -2 | -$\frac{3}{2}$ | -1 | 0 | 1 | $\frac{3}{2}$ | 2 | … |
| y=x3 | … | … |
（4）函数y=-x3+1的图象关于点（0，1）成中心对称图形．