题目内容
5. 如图,在△ABC中,点D为AC上一点,且$\frac{CD}{AD}=\frac{1}{2}$,过点D作DE∥BC交AB于点E,连接CE,过点D作DF∥CE交AB于点F.若AB=15,则EF=$\frac{10}{3}$.
如图,在△ABC中,点D为AC上一点,且$\frac{CD}{AD}=\frac{1}{2}$,过点D作DE∥BC交AB于点E,连接CE,过点D作DF∥CE交AB于点F.若AB=15,则EF=$\frac{10}{3}$.
分析 由DE与BC平行,由平行得比例求出AE的长,再由DF与CE平行,由平行得比例求出EF的长即可.
解答 解:∵DE∥BC,
∴$\frac{AD}{AC}$=$\frac{AE}{AB}$,
∵$\frac{CD}{AD}$=$\frac{1}{2}$,
∴$\frac{AD}{AC}$=$\frac{2}{3}$,即$\frac{AE}{AB}$=$\frac{2}{3}$,
∵AB=15,
∴AE=10,
∵DF∥CE,
∴$\frac{AF}{AE}$=$\frac{AD}{AC}$,即$\frac{AF}{10}$=$\frac{2}{3}$,
解得:AF=$\frac{20}{3}$,
则EF=AE-AF=10-$\frac{20}{3}$=$\frac{10}{3}$,
故答案为:$\frac{10}{3}$
点评 此题考查了平行线分线段成比例,熟练掌握平行线分线段成比例性质是解本题的关键.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案
相关题目
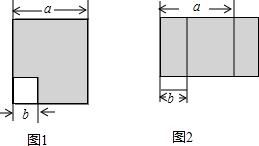
 现有八个大小相同的长方形,可拼成如图①、②所示的图形,在拼图②时,中间留下了一个边长为2的小正方形,则每个小正方形的面积是60.
现有八个大小相同的长方形,可拼成如图①、②所示的图形,在拼图②时,中间留下了一个边长为2的小正方形,则每个小正方形的面积是60. 如图,将正方形ABCD的边BC延长到E,使CE=AC,AE与DC交于点F,则CE:FC=$\sqrt{2}$+1.
如图,将正方形ABCD的边BC延长到E,使CE=AC,AE与DC交于点F,则CE:FC=$\sqrt{2}$+1.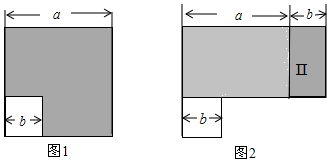
 如图,点M是边长为4cm的正方形的边AB的中点,点P是正方形边上的动点,从点M出发沿着逆时针方向在正方形的边上以每秒1cm的速度运动,则当点P逆时针旋转一周时,随着运动时间的增加,△DMP面积达到5cm2的时刻的个数是( )
如图,点M是边长为4cm的正方形的边AB的中点,点P是正方形边上的动点,从点M出发沿着逆时针方向在正方形的边上以每秒1cm的速度运动,则当点P逆时针旋转一周时,随着运动时间的增加,△DMP面积达到5cm2的时刻的个数是( )