题目内容
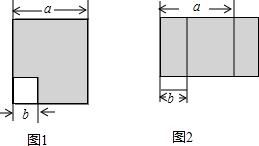
13．如图1，是边长为a的大正方形去掉一个边长为b的小正方形形成的，设其阴影部分面积为S1，将图1的阴影部分沿虚线剪开拼成的长方形如图2，拼接不重叠且无缝隙，设长方形面积为S2．（1）求S1和S2；（用含a，b的代数式表示）
（2）由S1和S2的关系可以得到的一个乘法公式为（a+b）（a-b）=a2-b2．．
分析 根据在边长为a的大正方形中剪去一个边长为b的小正方形，利用平方差公式即可得出答案．
解答 解：（1）由题意可得：${s}_{1}={a}^{2}-{b}^{2}，{s}_{2}=（a+b）（a-b）={a}^{2}-{b}^{2}$；
（2）所以可得公式：（a+b）（a-b）=a2-b2．
故答案为：（a+b）（a-b）=a2-b2．
点评 本题主要考查对平方差公式的知识点的理解和掌握，能根据根据在边长为a的大正方形中剪去一个边长为b的小正方形是解此题的关键．
练习册系列答案
相关题目
某小区有一块长方形的草地（如图），长18米，宽10米，空白部分为两条宽度均为2米的小路，则草地的实际面积128m2．
如图，在△ABC中，点D为AC上一点，且$\frac{CD}{AD}=\frac{1}{2}$，过点D作DE∥BC交AB于点E，连接CE，过点D作DF∥CE交AB于点F．若AB=15，则EF=$\frac{10}{3}$．
如图，在⊙O中，AB为直径，Rt△OBC的直角边OC=BC=1，过点C作直线DE∥AB交圆于D、E两点，BD与OC交于点F．
如图，点P1，P2，P3…P16是直线l上的16个点，则图中共有线段的条数是120．