题目内容
5.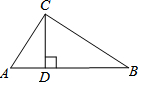 如图,在△ABC中,∠ACB=90°,CD⊥AB,垂足为D,若AC=6,BC=8,则CD等于( )
如图,在△ABC中,∠ACB=90°,CD⊥AB,垂足为D,若AC=6,BC=8,则CD等于( )| A. | 1 | B. | 2 | C. | 3 | D. | 4.8 |
分析 根据勾股定理求出AB,利用三角形的面积公式计算即可.
解答 解:∵∠ACB=90°,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=10,
$\frac{1}{2}$×AC×BC=$\frac{1}{2}$×AB×CD,即$\frac{1}{2}×$6×8=$\frac{1}{2}×$10×CD,
解得,CD=4.8,
故选:D.
点评 本题考查的是勾股定理的应用,掌握直角三角形的两条直角边长分别是a,b,斜边长为c,那么a2+b2=c2是解题的关键.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
15. 己知实数a,b在数轴上的位置如图所示,下列结论错误的是( )
己知实数a,b在数轴上的位置如图所示,下列结论错误的是( )
 己知实数a,b在数轴上的位置如图所示,下列结论错误的是( )
己知实数a,b在数轴上的位置如图所示,下列结论错误的是( )| A. | 1<|a|<b | B. | 1<-a<b | C. | |a|<1<|b| | D. | -b<a<-1 |
20.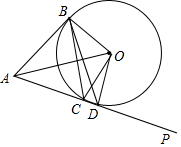 从⊙O外一点A作⊙O的切线,切点为B,作直线AP交⊙O于C、D两点,连接OA,OB,OC,OD,若∠ACB=60°,∠ADB=45°,则下列结论错误的是( )
从⊙O外一点A作⊙O的切线,切点为B,作直线AP交⊙O于C、D两点,连接OA,OB,OC,OD,若∠ACB=60°,∠ADB=45°,则下列结论错误的是( )
 从⊙O外一点A作⊙O的切线,切点为B,作直线AP交⊙O于C、D两点,连接OA,OB,OC,OD,若∠ACB=60°,∠ADB=45°,则下列结论错误的是( )
从⊙O外一点A作⊙O的切线,切点为B,作直线AP交⊙O于C、D两点,连接OA,OB,OC,OD,若∠ACB=60°,∠ADB=45°,则下列结论错误的是( )| A. | ∠COD=30° | B. | AB⊥OB | C. | AB∥OC | D. | ∠ABC=60° |
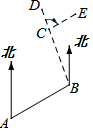 如图,小明从A出发沿北偏东60°方向行走至B处,又沿北偏西20°方向行走至C处,此时需把方向调整到与出发时一致,则方向的调整应是右转80°.
如图,小明从A出发沿北偏东60°方向行走至B处,又沿北偏西20°方向行走至C处,此时需把方向调整到与出发时一致,则方向的调整应是右转80°.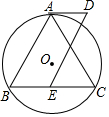 如图,⊙O是△ABC的外接圆,$\widehat{AB}$=$\widehat{AC}$,AD是⊙O的切线,点E是BC上一点,且BE=AD.
如图,⊙O是△ABC的外接圆,$\widehat{AB}$=$\widehat{AC}$,AD是⊙O的切线,点E是BC上一点,且BE=AD.