题目内容
8.一个多位数整数,a代表这个整数分出来的左边数,b代表这个整数分出来的右边数,其中a,b两部分数位相同,若$\frac{a+b}{2}$正好为剩下的中间数,则这个多位数就叫平衡数,例如:357满足$\frac{3+7}{2}$=5,233241满足$\frac{23+41}{2}$=32.
(1)写出一个三位平衡数和一个六位平衡数,并证明任意一个六位平衡数一定能被3整除;
(2)若一个三位平衡数后两位数减去百位数字之差为3的倍数,且这个平衡数为偶数,求这个三位数.
分析 (1)根据题意举例得到三位平衡数及六位平衡数,并根据题意设出六位平衡数,分解后验证即可;
(2)根据题意表示出这个三位数即可.
解答 解:(1)三位平衡数:例如321,六位平衡数:例如183654.
若有一个六位平衡数,由于a代表这个整数分出来的左边数,b代表这个整数分出来的右边数,其中a,b两部分数位相同,若$\frac{a+b}{2}$正好为剩下的中间数.
设六位平衡数为1000a+$\frac{a+b}{2}$×100+b
=10000a+50a+50b+b
=1050a+51b
=3(350a+17b),
∵a、b都是两位整数,
∴六位数一定能被3整除;
(2)设这个三位数百位上的数为a.十位上的数为b.个位上的数为c.
由题意a+c=2b ①,
10b+a-c=3n(n为整数) ②,
①+②得到4a+6c=3n,
∴4a是3的倍数,
∵c是偶数,a+c=2b,
∴a是偶数,
∴a=6,
∴c=0时,b=3,
c=2时,b=4,
c=4时,b=5,
c=6时,b=6,
c=8时,b=7,
∴三位数为630,642,654,666,678.
点评 此题考查了因式分解的应用,熟练掌握因式分解的方法是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
5.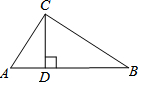 如图,在△ABC中,∠ACB=90°,CD⊥AB,垂足为D,若AC=6,BC=8,则CD等于( )
如图,在△ABC中,∠ACB=90°,CD⊥AB,垂足为D,若AC=6,BC=8,则CD等于( )
 如图,在△ABC中,∠ACB=90°,CD⊥AB,垂足为D,若AC=6,BC=8,则CD等于( )
如图,在△ABC中,∠ACB=90°,CD⊥AB,垂足为D,若AC=6,BC=8,则CD等于( )| A. | 1 | B. | 2 | C. | 3 | D. | 4.8 |
3.下列方程中的一元二次方程是( )
| A. | x2+x-$\frac{3}{x}$=0 | B. | x2-2x=x2 | C. | x2+y-1=0 | D. | x2-x-6=0 |
20.如图,四个全等的直角三角形纸片既可以拼成(内角不是直角)的菱形ABCD,也可以拼成正方形EFGH,则菱形ABCD面积和正方形EFGH面积之比为( )
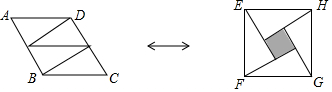

| A. | 1 | B. | $\frac{2\sqrt{5}}{5}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{2}{3}$ |
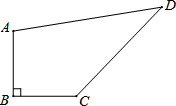 如图,四边形ABCD中,∠B=90°,AB=BC=3$\sqrt{2}$,CD=8,AD=10.
如图,四边形ABCD中,∠B=90°,AB=BC=3$\sqrt{2}$,CD=8,AD=10.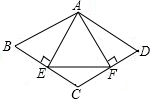 如图,平行四边形ABCD中,AE⊥BC,AF⊥CD,垂足分别为E,F,连结EF,给出下列判断:①若△AEF是等边三角形,则∠B=60°,②若∠B=60°,则△AEF是等边三角形,③若AE=AF,则平行四边形ABCD是菱形,④若平行四边形ABCD是菱形,则AE=AF,其中,结论正确的是①③④(只需填写正确结论的序号).
如图,平行四边形ABCD中,AE⊥BC,AF⊥CD,垂足分别为E,F,连结EF,给出下列判断:①若△AEF是等边三角形,则∠B=60°,②若∠B=60°,则△AEF是等边三角形,③若AE=AF,则平行四边形ABCD是菱形,④若平行四边形ABCD是菱形,则AE=AF,其中,结论正确的是①③④(只需填写正确结论的序号).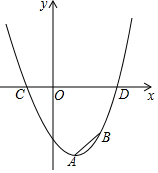 二次函数y=x2-2x-c 的图象如图所示,A,B两点的纵坐标分别为-4,-3,且AB=$\sqrt{2}$.
二次函数y=x2-2x-c 的图象如图所示,A,B两点的纵坐标分别为-4,-3,且AB=$\sqrt{2}$.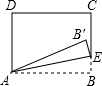 如图,矩形ABCD中,点E为射线BC上的一个动点,连接AE,以AE为对称轴折叠△AEB,得到△AEB′,点B的对称点为点B′,若AB=5,BC=3,当点B′落在射线CD上时,线段BE的长为$\frac{5}{3}$或15.
如图,矩形ABCD中,点E为射线BC上的一个动点,连接AE,以AE为对称轴折叠△AEB,得到△AEB′,点B的对称点为点B′,若AB=5,BC=3,当点B′落在射线CD上时,线段BE的长为$\frac{5}{3}$或15.