题目内容
20.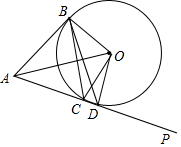 从⊙O外一点A作⊙O的切线,切点为B,作直线AP交⊙O于C、D两点,连接OA,OB,OC,OD,若∠ACB=60°,∠ADB=45°,则下列结论错误的是( )
从⊙O外一点A作⊙O的切线,切点为B,作直线AP交⊙O于C、D两点,连接OA,OB,OC,OD,若∠ACB=60°,∠ADB=45°,则下列结论错误的是( )| A. | ∠COD=30° | B. | AB⊥OB | C. | AB∥OC | D. | ∠ABC=60° |
分析 先计算出∠CBD=15°,则可根据圆周角定理对A进行判定;利用切线的性质可对B进行判断;根据圆周角定理得到∠BOC=2∠ADB=90°,则利用平行线的性质可对C进行判断;利用∠BOC=90°得到△BOC为等腰直角三角形,则∠OBC=45°,于是可对D进行判断.
解答 解:∵∠ACB=60°,∠ADB=45°,
∴∠CBD=15°,
∴∠COD=2∠CBD=30°,所以A选项的结论正确;
∵AB为切线,
∴AB⊥OB,所以B选项的结论正确;
∵∠BOC=2∠ADB=90°,
∴OC⊥OB,
∴AB∥OC,所以C选项的结论正确;
∵△BOC为等腰直角三角形,
∴∠OBC=45°,
∴∠ABC=90°-45°=45°,所以D选项的结论错误.
故选D.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.若出现圆的切线,必连过切点的半径,构造定理图,得出垂直关系.也考查了圆周角定理.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
5.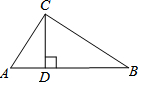 如图,在△ABC中,∠ACB=90°,CD⊥AB,垂足为D,若AC=6,BC=8,则CD等于( )
如图,在△ABC中,∠ACB=90°,CD⊥AB,垂足为D,若AC=6,BC=8,则CD等于( )
 如图,在△ABC中,∠ACB=90°,CD⊥AB,垂足为D,若AC=6,BC=8,则CD等于( )
如图,在△ABC中,∠ACB=90°,CD⊥AB,垂足为D,若AC=6,BC=8,则CD等于( )| A. | 1 | B. | 2 | C. | 3 | D. | 4.8 |
12.在数轴上表示不等式6x+4>3x-5的解集,正确的是( )
| A. |  | B. |  | C. |  | D. |  |
3.下列方程中的一元二次方程是( )
| A. | x2+x-$\frac{3}{x}$=0 | B. | x2-2x=x2 | C. | x2+y-1=0 | D. | x2-x-6=0 |