题目内容
 如图,已知∠DAB+∠D=180°,AC平分∠DAB,且∠CAD=25°,∠B=95°
如图,已知∠DAB+∠D=180°,AC平分∠DAB,且∠CAD=25°,∠B=95°(1)∠DCA的度数;
(2)∠DCE的度数;
(3)作BF垂直AC于F,求∠EBF的度数.
考点:平行线的判定与性质
专题:
分析:(1)利用角平分线的定义可以求得∠DAB的度数,再依据∠DAB+∠D=180°求得∠D的度数,在△ACD中利用三角形的内角和定理.即可求得∠DCA的度数;
(2)根据(1)可以证得:AB∥DC,利用平行线的性质定理即可求解;
(3)由三角形内角和定理和“直角三角形的两个锐角互余”进行解答.
(2)根据(1)可以证得:AB∥DC,利用平行线的性质定理即可求解;
(3)由三角形内角和定理和“直角三角形的两个锐角互余”进行解答.
解答: 解:(1)∵AC平分∠DAB,
解:(1)∵AC平分∠DAB,
∴∠CAB=∠DAC=25°,
∴∠DAB=50°,
∵∠DAB+∠D=180°,
∴∠D=180°-50°=130°,
∵△ACD中,∠D+∠DAC+∠DCA=180°,
∴∠DCA=180°-130°-25°=25°.
(2)∵∠DAC=25°,∠DCA=25°,
∴∠DAC=∠DCA,
∴AB∥DC,
∴∠DCE=∠B=95°;
(3)由(1)知,∠CAB=∠DAC=25°.
∵∠B=95°,
∴∠ACB=180°-25°-95°=60°.
又∵BF垂直AC于F,
∴∠CFB=90°,
∴∠CBF=90°-60°=30°,即∠EBF=30°.
 解:(1)∵AC平分∠DAB,
解:(1)∵AC平分∠DAB,∴∠CAB=∠DAC=25°,
∴∠DAB=50°,
∵∠DAB+∠D=180°,
∴∠D=180°-50°=130°,
∵△ACD中,∠D+∠DAC+∠DCA=180°,
∴∠DCA=180°-130°-25°=25°.
(2)∵∠DAC=25°,∠DCA=25°,
∴∠DAC=∠DCA,
∴AB∥DC,
∴∠DCE=∠B=95°;
(3)由(1)知,∠CAB=∠DAC=25°.
∵∠B=95°,
∴∠ACB=180°-25°-95°=60°.
又∵BF垂直AC于F,
∴∠CFB=90°,
∴∠CBF=90°-60°=30°,即∠EBF=30°.
点评:本题考查了平行线的判定与性质,以及三角形的内角和定理,正确证明AB∥DC是关键.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
 如图,在平面直角坐标中,以点C(0,4)为圆心,半径为4的圆交y轴正半轴于点A,AB是⊙C的切线,动点P从点A开始沿AB方向以每秒1个单位长度的速度运动,点Q从O点出发开始沿x轴正方向以每秒4个单位长度的速度运动,且动点P、Q同时出发,设运动时间为t(秒)
如图,在平面直角坐标中,以点C(0,4)为圆心,半径为4的圆交y轴正半轴于点A,AB是⊙C的切线,动点P从点A开始沿AB方向以每秒1个单位长度的速度运动,点Q从O点出发开始沿x轴正方向以每秒4个单位长度的速度运动,且动点P、Q同时出发,设运动时间为t(秒)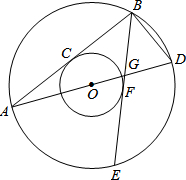 如图,两个同心圆的圆心是O,大圆的半径为10,小圆的半径为6,AD是大圆的直径.大圆的弦AB,BE分别与小圆相切于点C,F.AD,BE相交于点G,连接BD.
如图,两个同心圆的圆心是O,大圆的半径为10,小圆的半径为6,AD是大圆的直径.大圆的弦AB,BE分别与小圆相切于点C,F.AD,BE相交于点G,连接BD.