题目内容
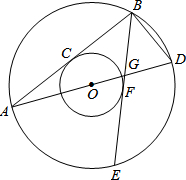 如图,两个同心圆的圆心是O,大圆的半径为10,小圆的半径为6,AD是大圆的直径.大圆的弦AB,BE分别与小圆相切于点C,F.AD,BE相交于点G,连接BD.
如图,两个同心圆的圆心是O,大圆的半径为10,小圆的半径为6,AD是大圆的直径.大圆的弦AB,BE分别与小圆相切于点C,F.AD,BE相交于点G,连接BD.(1)求BD的长;
(2)求∠ABE+2∠D的度数;
(3)求
| BG |
| AG |
考点:圆的综合题
专题:
分析:(1)连接OC,BD,AE,根据OC∥BD,OC为△ABD的中位线,可知:BD=2OC,得BD的长;
(2)连接AE,根据切线长定理知:AB=EB,可得:∠BAE=∠BEA;根据圆周角相等,得:∠D=∠AEB,可将∠ABE+2∠D的值求出;
(3)根据△BGO∽△AGB,可将
的值求出.
(2)连接AE,根据切线长定理知:AB=EB,可得:∠BAE=∠BEA;根据圆周角相等,得:∠D=∠AEB,可将∠ABE+2∠D的值求出;
(3)根据△BGO∽△AGB,可将
| BG |
| AG |
解答: 解:(1)连接OC,并延长BO交AE于点H,
解:(1)连接OC,并延长BO交AE于点H,
∵AB是小圆的切线,C是切点,
∴OC⊥AB,
∴C是AB的中点.
∵AD是大圆的直径,
∴O是AD的中点.
∴OC是△ABD的中位线.
∴BD=2OC=12;
(2)连接AE,由(1)知C是AB的中点.
同理F是BE的中点.
由切线长定理得BC=BF.
∴BA=BE.
∴∠BAE=∠E.
∵∠E=∠D,
∴∠ABE+2∠D=∠ABE+∠E+∠BAE=180°;
(3)连接BO,在Rt△OCB中,
∵OB=10,OC=6,
∴BC=8.
由(2)知∠OBG=∠OBC=∠OAC.
∵∠BGO=∠AGB,
∴△BGO∽△AGB.
∴
=
=
.
 解:(1)连接OC,并延长BO交AE于点H,
解:(1)连接OC,并延长BO交AE于点H,∵AB是小圆的切线,C是切点,
∴OC⊥AB,
∴C是AB的中点.
∵AD是大圆的直径,
∴O是AD的中点.
∴OC是△ABD的中位线.
∴BD=2OC=12;
(2)连接AE,由(1)知C是AB的中点.
同理F是BE的中点.
由切线长定理得BC=BF.
∴BA=BE.
∴∠BAE=∠E.
∵∠E=∠D,
∴∠ABE+2∠D=∠ABE+∠E+∠BAE=180°;
(3)连接BO,在Rt△OCB中,
∵OB=10,OC=6,
∴BC=8.
由(2)知∠OBG=∠OBC=∠OAC.
∵∠BGO=∠AGB,
∴△BGO∽△AGB.
∴
| BG |
| AG |
| OB |
| AB |
| 5 |
| 8 |
点评:本题考查了圆的综合题.在解本题的过程中要用到切线长定理,中位线定理,相似三角形的判定等知识,要求学生熟练掌握和应用.

练习册系列答案
 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
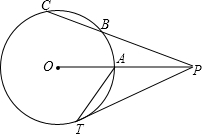 P为以r为半径的⊙O外一点,T是⊙O上一点,PO交⊙O于A点,cos∠OPT=
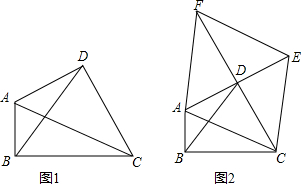
P为以r为半径的⊙O外一点,T是⊙O上一点,PO交⊙O于A点,cos∠OPT= 如图,已知∠DAB+∠D=180°,AC平分∠DAB,且∠CAD=25°,∠B=95°
如图,已知∠DAB+∠D=180°,AC平分∠DAB,且∠CAD=25°,∠B=95° 如图:在等腰直角三角形中,AB=AC,点D是斜边BC上的中点,点E、F分别为AB,AC上的点,且DE⊥DF.
如图:在等腰直角三角形中,AB=AC,点D是斜边BC上的中点,点E、F分别为AB,AC上的点,且DE⊥DF.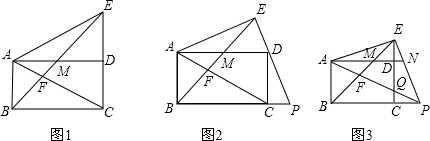
 如图,在△ABC中,BC=6,E、F分别是AB、AC的中点,动点P在射线EF上,BP交CE于D,∠CBP的平分线交CE于Q.
如图,在△ABC中,BC=6,E、F分别是AB、AC的中点,动点P在射线EF上,BP交CE于D,∠CBP的平分线交CE于Q.