题目内容
某商场将进货价为30元的台灯以40元的价格售出,平均每月能售出600个,经调查表明,单价在60元以内,这种台灯的售价每上涨1元,其销量就减少10个,
(1)为了实现销售这种台灯平均每月10000元的销售利润,售价应定为多少元?
(2)若商场要获得最大利润,则应上涨多少元?
(1)为了实现销售这种台灯平均每月10000元的销售利润,售价应定为多少元?
(2)若商场要获得最大利润,则应上涨多少元?
考点:二次函数的应用,一元二次方程的应用
专题:销售问题
分析:(1)设这种台灯上涨了x元,台灯将少售出10x,那么利润为(40+x-30)(600-10x)=10000,解方程即可;
(2)根据销售利润=每个台灯的利润×销售量,每个台灯的利润=售价-进价,关键是用售价x表示销售量.列出二次函数,用二次函数的性质,求最大值.
(2)根据销售利润=每个台灯的利润×销售量,每个台灯的利润=售价-进价,关键是用售价x表示销售量.列出二次函数,用二次函数的性质,求最大值.
解答:解:(1)设这种台灯上涨了x元.
(40+x-30)(600-10x)=10000
x2-50x+400=0
x=40(舍去)或x=10
40+10=50(元)
答:这种台灯的售价应定为50元.
(2)设台灯的售价为x元,利润为y元,依题意:
y=(x-30)[600-10(x-40)],
∴y=-10x2+1300x-30000
当x=65时,y最大=12250元,
即商场要获得最大利润,则应上涨65-40=25元.
答:商场要获得最大利润,则应上涨25元.
(40+x-30)(600-10x)=10000
x2-50x+400=0
x=40(舍去)或x=10
40+10=50(元)
答:这种台灯的售价应定为50元.
(2)设台灯的售价为x元,利润为y元,依题意:
y=(x-30)[600-10(x-40)],
∴y=-10x2+1300x-30000
当x=65时,y最大=12250元,
即商场要获得最大利润,则应上涨65-40=25元.
答:商场要获得最大利润,则应上涨25元.
点评:此题考查一元二次方程和二次函数的实际运用,通过由实际问题--一元二次方程(二次函数)--实际问题,三个阶段的探究,使学生体会到数学的运用价值,能提高学习兴趣.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 如图,已知AD∥BC,∠1=∠2,∠3=∠4,试问AB与DC平行吗?并说明理由.
如图,已知AD∥BC,∠1=∠2,∠3=∠4,试问AB与DC平行吗?并说明理由.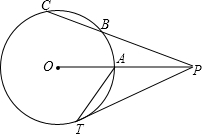 P为以r为半径的⊙O外一点,T是⊙O上一点,PO交⊙O于A点,cos∠OPT=
P为以r为半径的⊙O外一点,T是⊙O上一点,PO交⊙O于A点,cos∠OPT= 如图,已知∠DAB+∠D=180°,AC平分∠DAB,且∠CAD=25°,∠B=95°
如图,已知∠DAB+∠D=180°,AC平分∠DAB,且∠CAD=25°,∠B=95° 如图:在等腰直角三角形中,AB=AC,点D是斜边BC上的中点,点E、F分别为AB,AC上的点,且DE⊥DF.
如图:在等腰直角三角形中,AB=AC,点D是斜边BC上的中点,点E、F分别为AB,AC上的点,且DE⊥DF.