题目内容
17.下面是李刚同学在一次测验中解答的填空题,其中答对的是( )| A. | 若x2=4,则x=2 | |
| B. | 方程x2=x的解为x=1 | |
| C. | 若x2+2x+k=0有一根为2,则k=-8 | |
| D. | 若分式$\frac{{{x^2}-3x+2}}{x-1}$值为零,则x=1,2 |
分析 利用直接开平方法解方程可对A进行判断;利用因式分解法解方程可对B进行判断;根据一元二次方程解的定义把x=2代入方程可求出k,则可对C进行判断;根据分式有意义的条件可对D进行判断.
解答 解:A、若x2=4,则x1=2,x2=-2,所以A选项错误;
B、x2=x,则x(x-1)=0,所以x1=0,x2=1,所以B选项错误;
C、若x2+2x+k=0有一根为2,则4+4+k=0,所以k=-8,所以C选项错误;
D、分式$\frac{{{x^2}-3x+2}}{x-1}$值为零,x2-3x+2=0且x-1≠0,则x=2,所以D选项错误.
故选C.
点评 本题考查了解一元二次方程-因式分解法:先把方程的右边化为0,再把左边通过因式分解化为两个一次因式的积的形式,那么这两个因式的值就都有可能为0,这就能得到两个一元一次方程的解,这样也就把原方程进行了降次,把解一元二次方程转化为解一元一次方程的问题了(数学转化思想).也考查了分式有意义的条件.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
7.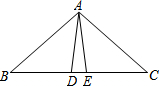 如图所示,AD=AE,BD=CE,∠ADB=AEC=100°,∠BAE=70°,下列结论错误的是( )
如图所示,AD=AE,BD=CE,∠ADB=AEC=100°,∠BAE=70°,下列结论错误的是( )
 如图所示,AD=AE,BD=CE,∠ADB=AEC=100°,∠BAE=70°,下列结论错误的是( )
如图所示,AD=AE,BD=CE,∠ADB=AEC=100°,∠BAE=70°,下列结论错误的是( )| A. | △ABE≌△ACD | B. | △ABD≌△ACE | C. | ∠C=30° | D. | ∠DAE=40° |
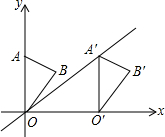 如图,在平面直角坐标系中,点A的坐标为(0,4),△OAB沿x轴向右平移后得到△0′A′B′,A的对应点A′是直线y=$\frac{4}{5}$x上一点,则点B与其对应点B′间的距离为( )
如图,在平面直角坐标系中,点A的坐标为(0,4),△OAB沿x轴向右平移后得到△0′A′B′,A的对应点A′是直线y=$\frac{4}{5}$x上一点,则点B与其对应点B′间的距离为( )