题目内容
5.已知抛物线C1:y=ax2+4ax+4a+b(a≠0,b>0)的顶点为M,经过原点O且与x轴另一交点为A.(1)求点A的坐标;
(2)若△AMO为等腰直角三角形,求抛物线C1的解析式;
(3)现将抛物线C1绕着点P(m,0)旋转180°后得到抛物线C2,若抛物线C2的顶点为N,当b=1,且顶点N在抛物线C1上时,求m的值.
分析 (1)由抛物线经过原点可知当x=0时,y=0,由此可得关于x的一元二次方程,解方程即可求出抛物线x轴另一交点坐标;
(2)由△AMO为等腰直角三角形,抛物线的顶点为M,可求出b的值,再把原点坐标(0,0)代入求出a的值,即可求出抛物线C1的解析式;
(3)由b=1,易求线抛物线C1的解析式,设N(n,-1),再由点P(m,0)可求出n和m的关系,当顶点N在抛物线C1上可把N的坐标代入抛物线即可求出m的值.
解答 解:(1)∵抛物线C1:y=ax2+4ax+4a+b(a≠0,b>0)经过原点O,
∴0=4a+b,
∴当ax2+4ax+4a+b=0时,则ax2+4ax=0,
解得:x=0或-4,
∴抛物线与x轴另一交点A坐标是(-4,0);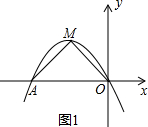 (2)∵抛物线C1:y=ax2+4ax+4a+b=a(x+2)2+b(a≠0,b>0),(如图1)
(2)∵抛物线C1:y=ax2+4ax+4a+b=a(x+2)2+b(a≠0,b>0),(如图1)
∴顶点M坐标为(-2,b),
∵△AMO为等腰直角三角形,
∴b=2,
∵抛物线C1:y=ax2+4ax+4a+b=a(x+2)2+b过原点,
∴a(0+2)2+2=0,
解得:a=-$\frac{1}{2}$,
∴抛物线C1:y=-$\frac{1}{2}$x2-2x;
(3)∵b=1,抛物线C1:y=ax2+4ax+4a+b=a(x+2)2+b过原点,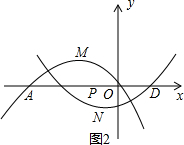 (如图2)
(如图2)
∴a=-$\frac{1}{4}$,
∴y=-$\frac{1}{4}$(x+2)2+1=-$\frac{1}{4}$x2-x,
设N(n,-1),又因为点P(m,0),
∴n-m=m+2,
∴n=2m+2
即点N的坐标是(2m+2,-1),
∵顶点N在抛物线C1上,
∴-1=-$\frac{1}{4}$(2m+2+2)2+1,
解得:m=-2+$\sqrt{2}$或-2-$\sqrt{2}$.
点评 本题考查了二次函数图象与几何变换.由于抛物线旋转后的形状不变,故|a|不变,所以求旋转移后的抛物线解析式通常可利用两种方法:一是求出原抛物线上任意两点旋转移后的坐标,利用待定系数法求出解析式;二是只考虑旋转后的顶点坐标,即可求出解析式.

 天天练口算系列答案
天天练口算系列答案| A. | 对角线相等且互相垂直的四边形是正方形 | |
| B. | 两个底角相等的梯形是等腰梯形 | |
| C. | 对角线相等的四边形是矩形 | |
| D. | 对角线互相垂直且互相平分的四边形是菱形 |
| A. | 若x2=4,则x=2 | |
| B. | 方程x2=x的解为x=1 | |
| C. | 若x2+2x+k=0有一根为2,则k=-8 | |
| D. | 若分式$\frac{{{x^2}-3x+2}}{x-1}$值为零,则x=1,2 |
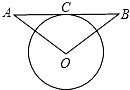 如图,AB与⊙O相切于点C,OA-=OB,⊙O的直径为6cm,AB=8cm,求sinA的值.
如图,AB与⊙O相切于点C,OA-=OB,⊙O的直径为6cm,AB=8cm,求sinA的值.