Question

13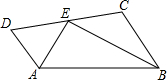．已知，如图，AD∥BC，AE平分∠BAD，BE平分∠ABC，求证：AD+BC=AB．
提示；解决这类问题有两种思路：
（1）在AB上取AF=AD，然后通过证明△BFE≌△BCE，得BF=BC，这是截长法．
（2）延长AD交BE的延长线于G，先证△AGE≌△ABE，后证△DGE≌△CBE，即可证得AD+BC=AB，这是补短法．

Answer 1

分析 解决这类问题有两种思路：（1）在AB上取AF=AD，然后通过证明△BFE≌△BCE，得BF=BC，这是截长法；（2）延长AD交BE的延长线于G，先证△AGE≌△ABE，后证△DGE≌△CBE，即可证得AD+BC=AB，这是补短法．

解答 证法一：在AB上截取AF=AD，连接EF，
∵AE平分∠BAD，
∴∠DAE=∠FAE，
由AF=AD，∠DAE=∠FAE，AE=AE，可得△ADE≌△AFE（SAS），
∴∠DEA=∠FEA，
∵AD∥BC，AE平分∠BAD，BE平分∠ABC，
∴∠EAB+∠EBA=$\frac{1}{2}$（∠DAB+∠CBA）=$\frac{1}{2}$×180°=90°，∠CBE=∠FBE，
∴∠AEB=90°，
∴∠AED+∠BEC=90°，∠AEF+∠BFE=90°，
∴∠BEC=∠BEF，
由∠BEC=∠BEF，BE=BE，∠CBE=∠FBE，可得△BFE≌△BCE，
∴BF=BC，
∴AB=AF+BF=AD+BC；

证法二：延长AD交BE的延长线于G，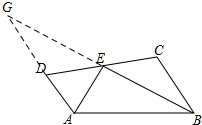
∵AD∥BC，EB平分∠ABC，
∴∠G=∠CBE，∠ABE=∠CBE，
∴∠G=∠ABE，
∵EA平分BAD，
∴GAE=∠BAE，
由∠G=∠ABE，GAE=∠BAE，AE=AE，可得△AEG≌△AEB，
∴AG=AB=AD+DG，BE=GE，
由∠G=∠CBE，BE=GE，∠GED=∠BEC，可得△DGE≌△CEB，
∴DG=BC，
∴AB=AD+BC．

点评 本题主要考查了全等三角形的判定与性质，解决问题的关键是作辅助线构造全等三角形，根据全等三角形的对应边相等得出结论．在判定三角形全等时，关键是选择恰当的判定条件．