题目内容
5.已知抛物线y=-$\frac{2}{3}$x2(1)判断点A(-1,$\frac{2}{3}$),B($\frac{3}{2}$,-$\frac{3}{2}$)是否在此抛物线上;
(2)若点C($\frac{1}{2}$,a),D(b,-$\frac{1}{3}$)都在此抛物线上,求a,b的值
(3)若E(x1,y1),点F(x2,y2)都在此抛物线上,且x1>x2>0,试比较y1与y2的大小.
分析 (1)把A、B两点的坐标分别代入函数解析式判断即可;
(2)把C、D两点的坐标分别代入函数解析式可求得a、b的值;
(3)利用二次函数的增减性进行比较即可.
解答 解:
(1)当x=-1时,y=-$\frac{2}{3}$×(-1)2=-$\frac{2}{3}$≠$\frac{2}{3}$,故A点不在抛物线上,
当x=$\frac{3}{2}$时,y=-$\frac{2}{3}$×($\frac{3}{2}$)2=-$\frac{3}{2}$,故B点在抛物线上;
(2)∵点C($\frac{1}{2}$,a)在此抛物线上,
∴a=-$\frac{2}{3}$×($\frac{1}{2}$)2=-$\frac{1}{6}$,
∵D(b,-$\frac{1}{3}$)在此抛物线上,
∴-$\frac{1}{3}$=-$\frac{2}{3}$b2,解得b=±$\frac{\sqrt{2}}{2}$;
(3)∵y=-$\frac{2}{3}$x2,
∴抛物线开口向下,当x>0时,y随x的增大而减小,
∵x1>x2>0,
∴y1<y2.
点评 本题主要考查二次函数的性质,掌握二次函数图象上的点的坐标满足函数解析式是解题的关键.

练习册系列答案
相关题目
1.已知Rt△ABC的直角边AC=BC=4cm,若以C为圆心,以3cm为半径作圆,则这个圆与斜边AB所在直线的位置关系是( )
| A. | 相交 | B. | 相切 | C. | 相离 | D. | 不能确定 |
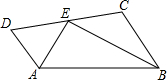 已知,如图,AD∥BC,AE平分∠BAD,BE平分∠ABC,求证:AD+BC=AB.
已知,如图,AD∥BC,AE平分∠BAD,BE平分∠ABC,求证:AD+BC=AB.