题目内容
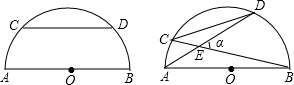
19．
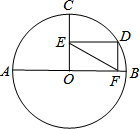如图，⊙O的直径AB=4，半径OC⊥AB，点D在弧BC上，DE⊥OC，DF⊥AB，垂足分别为E、F，则OE•OF满足（ ）| A． | OE•OF≤1 | B． | OE•OF≤2 | C． | OE•OF≤3 | D． | OE•OF≤4 |
分析 先由勾股定理得出OE2+OF2=EF2，再证明四边形OFDE是矩形，根据矩形的对角线相等得出EF=OD=2，然后利用不等式的性质解答即可．
解答 解：∵OC⊥AB，
∴OE2+OF2=EF2，
∵OC⊥AB，DE⊥OC，DF⊥AB，
∴四边形OFDE是矩形，
∴EF=OD=2，
∴OE2+OF2=4，
∴OE•OF≤$\frac{1}{2}$（OE2+OF2）=2．
故选B．
点评 本题考查了勾股定理，矩形的判定与性质，圆的认识，不等式的性质，利用矩形的对角线相等把EF转化为OD是解题的关键．
练习册系列答案
相关题目
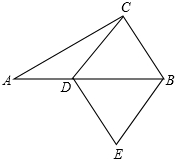如图，在Rt△ABC中，∠ACB=90°，AC=4，BC=3，D为AB上一点，以CD，CB边作菱形CDEB，求AD的长．
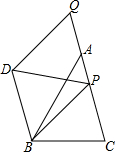如图，在△ABC中，AB=6，tan∠BAC=$\frac{3}{4}$，点P为AC边上任意一点，点Q为CA延长线上任意一点，以PB、PQ为两边作?PQDB，则对角线PD的最小值为$\frac{18}{5}$．
如图，点O是△ABC的边BC的中点，且点O到△ABC的两边AB，AC所在的直线的距离相等，求证：AB=AC．