题目内容
11.如图,AB是半圆O的直径,AB=10,C、D是半圆上两个动点,且始终保持线段CD=8.(1)当CD∥AB时,求CD与AB之间的距离;
(2)在C、D运动的过程中,AD与BC交于点E,∠BED=α,α值是否是定值?若不是,说明理由;若是,求出tanα.
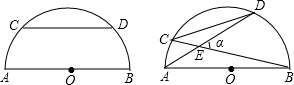
分析 (1)如图1,过O作OE⊥CD于E,连接OC,根据垂径定理得到CE=$\frac{1}{2}$CD=4,根据勾股定理即可得到结论;
(2)α值是定值,如图2,连接BD,根据△CDE∽△ABE,求得$\frac{DE}{BE}$=$\frac{CD}{AB}$=$\frac{4}{5}$,于是得到cos∠α=$\frac{DE}{BE}$=$\frac{4}{5}$,推出α值是定值,根据勾股定理得到BD=$\sqrt{B{E}^{2}-D{E}^{2}}$=3k.即可的结论.
解答 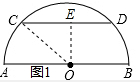 解:(1)如图1,过O作OE⊥CD于E,连接OC,
解:(1)如图1,过O作OE⊥CD于E,连接OC,
∴CE=$\frac{1}{2}$CD=4,
∴OE=$\sqrt{O{C}^{2}-C{E}^{2}}$=3,
∴CD与AB之间的距离是3;
(2)α值是定值,如图2,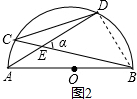 连接BD,
连接BD,
∵∠C=∠DAB,∠CDA=∠ABC,
∴△CDE∽△ABE,
∴$\frac{DE}{BE}$=$\frac{CD}{AB}$=$\frac{4}{5}$,
∵AB是半圆O的直径,
∴∠ADB=90°,
∴cos∠α=$\frac{DE}{BE}$=$\frac{4}{5}$,
∴α值是定值,
设DE=4k,BE=5k,
∴BD=$\sqrt{B{E}^{2}-D{E}^{2}}$=3k.
∴tanα=$\frac{BD}{DE}$=$\frac{3k}{4k}$=$\frac{3}{4}$.
点评 本题考查了垂径定理,圆周角定理,相似三角形的判定和性质,正确的作出辅助线是解题的关键.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案
相关题目
19.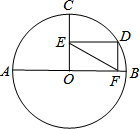 如图,⊙O的直径AB=4,半径OC⊥AB,点D在弧BC上,DE⊥OC,DF⊥AB,垂足分别为E、F,则OE•OF满足( )
如图,⊙O的直径AB=4,半径OC⊥AB,点D在弧BC上,DE⊥OC,DF⊥AB,垂足分别为E、F,则OE•OF满足( )
 如图,⊙O的直径AB=4,半径OC⊥AB,点D在弧BC上,DE⊥OC,DF⊥AB,垂足分别为E、F,则OE•OF满足( )
如图,⊙O的直径AB=4,半径OC⊥AB,点D在弧BC上,DE⊥OC,DF⊥AB,垂足分别为E、F,则OE•OF满足( )| A. | OE•OF≤1 | B. | OE•OF≤2 | C. | OE•OF≤3 | D. | OE•OF≤4 |
6.某城市十月末连续四天的天气情况如图所示,这四天中温差(最高气温与最低气温的差)最大的是( )


| A. | 星期一 | B. | 星期二 | C. | 星期三 | D. | 星期四 |
3.甲数比乙数的$\frac{1}{4}$还多1,设乙数为x,则甲数可表示为( )
| A. | $\frac{1}{4}x+1$ | B. | 4x-1 | C. | 4(x-1) | D. | 4(x+1) |
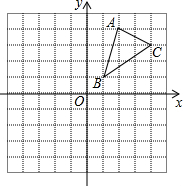 如图,△ABC三个顶点的坐标分别为A(2,4),B(1,1),C(4,3).
如图,△ABC三个顶点的坐标分别为A(2,4),B(1,1),C(4,3).