题目内容
8.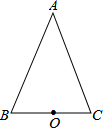 如图,点O是△ABC的边BC的中点,且点O到△ABC的两边AB,AC所在的直线的距离相等,求证:AB=AC.
如图,点O是△ABC的边BC的中点,且点O到△ABC的两边AB,AC所在的直线的距离相等,求证:AB=AC.
分析 求证AB=AC,就是求证∠B=∠C,可通过构建全等三角形来求.过点O分别作OE⊥AB于E,OF⊥AC于F,那么可以用斜边直角边定理(HL)证明Rt△OEB≌Rt△OFC来实现.
解答 证明:过点O分别作OE⊥AB于E,OF⊥AC于F,
由题意知,
在Rt△OEB和Rt△OFC中
$\left\{\begin{array}{l}{OB=OC}\\{OE=OF}\end{array}\right.$
∴Rt△OEB≌Rt△OFC(HL),
∴∠ABC=∠ACB,
∴AB=AC.
点评 题的关键是通过辅助线来构建全等三角形.判定两个三角形全等,先根据已知条件或求证的结论确定三角形,然后再根据三角形全等的判定方法,看缺什么条件,再去证什么条件.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
19.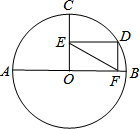 如图,⊙O的直径AB=4,半径OC⊥AB,点D在弧BC上,DE⊥OC,DF⊥AB,垂足分别为E、F,则OE•OF满足( )
如图,⊙O的直径AB=4,半径OC⊥AB,点D在弧BC上,DE⊥OC,DF⊥AB,垂足分别为E、F,则OE•OF满足( )
 如图,⊙O的直径AB=4,半径OC⊥AB,点D在弧BC上,DE⊥OC,DF⊥AB,垂足分别为E、F,则OE•OF满足( )
如图,⊙O的直径AB=4,半径OC⊥AB,点D在弧BC上,DE⊥OC,DF⊥AB,垂足分别为E、F,则OE•OF满足( )| A. | OE•OF≤1 | B. | OE•OF≤2 | C. | OE•OF≤3 | D. | OE•OF≤4 |
3.甲数比乙数的$\frac{1}{4}$还多1,设乙数为x,则甲数可表示为( )
| A. | $\frac{1}{4}x+1$ | B. | 4x-1 | C. | 4(x-1) | D. | 4(x+1) |
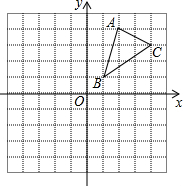 如图,△ABC三个顶点的坐标分别为A(2,4),B(1,1),C(4,3).
如图,△ABC三个顶点的坐标分别为A(2,4),B(1,1),C(4,3).