题目内容
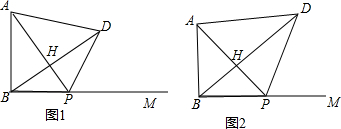
7.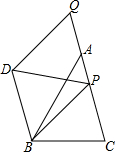 如图,在△ABC中,AB=6,tan∠BAC=$\frac{3}{4}$,点P为AC边上任意一点,点Q为CA延长线上任意一点,以PB、PQ为两边作?PQDB,则对角线PD的最小值为$\frac{18}{5}$.
如图,在△ABC中,AB=6,tan∠BAC=$\frac{3}{4}$,点P为AC边上任意一点,点Q为CA延长线上任意一点,以PB、PQ为两边作?PQDB,则对角线PD的最小值为$\frac{18}{5}$.
分析 由题意可知当PD⊥BD时,对角线PD的最小值,过点A作AE⊥BD于点E,利用平行四边形的性质和已知条件即可求出PD的长.
解答 解:由题意可知当PD⊥BD时,对角线PD的最小值,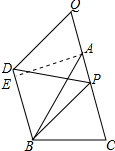
∵四边形PQDB是平行四边形
∴PQ∥BD,
∴∠ABD=∠BAC,
∵tan∠BAC=$\frac{3}{4}$,
∴sin∠BAC=$\frac{3}{5}$=sin∠ABD,
过点A作AE⊥BD于点E,如图所示:
∴当PD最小时,PD=AE,
∴AE=AB•sin∠ABE=AB•sin∠BAC
=6×$\frac{3}{5}$=$\frac{18}{5}$,
∴对角线PD的最小值为$\frac{18}{5}$,
故答案为:$\frac{18}{5}$.
点评 本题考查了平行四边形的性质以及垂线段最短的性质,解题的关键是当PD最小时,PD=AE,求PE的长,转化为求线段AE的长.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
19.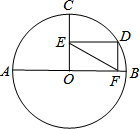 如图,⊙O的直径AB=4,半径OC⊥AB,点D在弧BC上,DE⊥OC,DF⊥AB,垂足分别为E、F,则OE•OF满足( )
如图,⊙O的直径AB=4,半径OC⊥AB,点D在弧BC上,DE⊥OC,DF⊥AB,垂足分别为E、F,则OE•OF满足( )
 如图,⊙O的直径AB=4,半径OC⊥AB,点D在弧BC上,DE⊥OC,DF⊥AB,垂足分别为E、F,则OE•OF满足( )
如图,⊙O的直径AB=4,半径OC⊥AB,点D在弧BC上,DE⊥OC,DF⊥AB,垂足分别为E、F,则OE•OF满足( )| A. | OE•OF≤1 | B. | OE•OF≤2 | C. | OE•OF≤3 | D. | OE•OF≤4 |
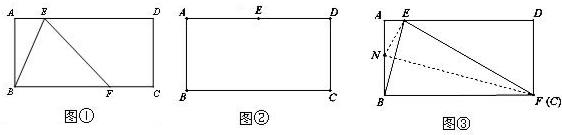
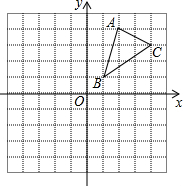 如图,△ABC三个顶点的坐标分别为A(2,4),B(1,1),C(4,3).
如图,△ABC三个顶点的坐标分别为A(2,4),B(1,1),C(4,3).