题目内容
12.已知三角形三条边的长度分别是:①1,$\sqrt{2}$,$\sqrt{3}$;②2,3,4;③3n,4n,5n(n>0);④32,42,52.其中一定能构成直角三角形的有( )| A. | 1组 | B. | 2组 | C. | 3组 | D. | 4组 |
分析 先求得三边的平方,再验证两小边的平方和等于最长边的平方即可.
解答 解:①12+($\sqrt{2}$)2=($\sqrt{3}$)2,故是直角三角形,正确;
②22+32≠42,故不是直角三角形,错误;
③(3n)2+(4n)2=(5n)2,故是直角三角形,正确;
④(32)2+(42)2≠(52)2,故不是直角三角形,错误.
故选B.
点评 本题考查了勾股定理的逆定理,在应用勾股定理的逆定理时,应先认真分析所给边的大小关系,确定最大边后,再验证两条较小边的平方和与最大边的平方之间的关系,进而作出判断.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
17.下列计算中,正确的是( )
| A. | 2a(3a-1)=6a3-1 | B. | x•x3=x3 | C. | (-2xy2)4=16x4y8 | D. | x3+x3=x6 |
4. 已知实数a在数轴上的位置如图所示,则化简|a-1|+$\sqrt{{a}^{2}}$的结果是( )
已知实数a在数轴上的位置如图所示,则化简|a-1|+$\sqrt{{a}^{2}}$的结果是( )
 已知实数a在数轴上的位置如图所示,则化简|a-1|+$\sqrt{{a}^{2}}$的结果是( )
已知实数a在数轴上的位置如图所示,则化简|a-1|+$\sqrt{{a}^{2}}$的结果是( )| A. | -1 | B. | 1 | C. | 1-2a | D. | 2a-1 |
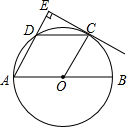 如图所示,AB是⊙O的直径,点C是$\widehat{BD}$的中点,∠COB=60°,过点C作CE⊥AD,交AD的延长线于点E
如图所示,AB是⊙O的直径,点C是$\widehat{BD}$的中点,∠COB=60°,过点C作CE⊥AD,交AD的延长线于点E 如图,在?ABCD中,点E、F在对角线BD的延长线上,且ED=FB,连结AE、EC、CF,AF.
如图,在?ABCD中,点E、F在对角线BD的延长线上,且ED=FB,连结AE、EC、CF,AF. 如图,在Rt△ABC中,∠ACB=90°,D、E、F分别是AB、BC、CA的中点,若CD=5cm,求EF的长.
如图,在Rt△ABC中,∠ACB=90°,D、E、F分别是AB、BC、CA的中点,若CD=5cm,求EF的长.