题目内容
20.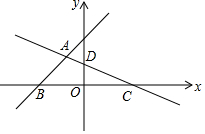 如图,在平面直角坐标系中,直线y=x+3与x轴交于点B,与直线CD交于点A(-$\frac{12}{11}$,a),点D的坐标为(0,$\frac{3}{2}$),点C在x轴上
如图,在平面直角坐标系中,直线y=x+3与x轴交于点B,与直线CD交于点A(-$\frac{12}{11}$,a),点D的坐标为(0,$\frac{3}{2}$),点C在x轴上(1)求a的值;
(2)求直线CD的解析式;
(3)若点E是直线CD上一动点(不与点C重合),当△CBE∽△COD时,求点E的坐标.
分析 (1)将点A的横坐标代入直线y=x+3中即可求出a;
(2)用待定系数法直接求出直线CD的解析式;
(3)先由两三角形相似即可得出∠CBE=90°,进而得出点E的横坐标,再代入直线CD的解析式中,即可得出结论.
解答 解:(1)∵点A(-$\frac{12}{11}$,a)在直线y=x+3上,
∴-$\frac{12}{11}$+3=a,
∴a=$\frac{21}{11}$,
(2)∵D(0,$\frac{3}{2}$),
∴设直线CD的解析式为y=kx+$\frac{3}{2}$(k≠0),
由(1)知,a=$\frac{21}{11}$,
∴A(-$\frac{12}{11}$,$\frac{21}{11}$),
∵点A在直线CD上,
∴$\frac{21}{11}$=-$\frac{12}{11}$k+$\frac{3}{2}$,
∴k=-$\frac{3}{8}$,
∴直线CD的解析式为y=-$\frac{3}{8}$x+$\frac{3}{2}$;
(3)∵点B是直线y=x+3与x轴的交点,
∴B(-3,0),
∵△CBE∽△COD,
∴∠CBE=∠COD=90°,
∴点E的横坐标为-3,
当x=-3时,y=-$\frac{3}{8}$×(-3)+$\frac{3}{2}$=$\frac{21}{8}$,
∴E(-3,$\frac{21}{8}$).
点评 此题是一次函数综合题,主要考查了待定系数法求直线解析式,相似三角形的性质,解本题的关键是求出直线CD的解析式,是一道比较简单的题目.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.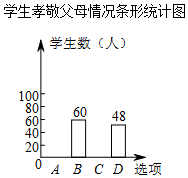 某校为了了解学生孝敬父母的情况(选项:A.为父母洗一次脚;B.帮父母做一次家务;C.给父母买一件礼物;D.其它),在全校范围内随机抽取了若干名学生进行调查,得到如图表(部分信息未给出):根据以上信息解答下列问题:
某校为了了解学生孝敬父母的情况(选项:A.为父母洗一次脚;B.帮父母做一次家务;C.给父母买一件礼物;D.其它),在全校范围内随机抽取了若干名学生进行调查,得到如图表(部分信息未给出):根据以上信息解答下列问题:
学生孝敬父母情况统计表:
(1)表中m=36,n=96,p=0.25.
(2)这次被调查的学生有多少人?并补全条形统计图.
(3)该校有1600名学生,估计该校全体学生中选择B选项的有多少人?
 某校为了了解学生孝敬父母的情况(选项:A.为父母洗一次脚;B.帮父母做一次家务;C.给父母买一件礼物;D.其它),在全校范围内随机抽取了若干名学生进行调查,得到如图表(部分信息未给出):根据以上信息解答下列问题:
某校为了了解学生孝敬父母的情况(选项:A.为父母洗一次脚;B.帮父母做一次家务;C.给父母买一件礼物;D.其它),在全校范围内随机抽取了若干名学生进行调查,得到如图表(部分信息未给出):根据以上信息解答下列问题:学生孝敬父母情况统计表:
| 选项 | 频数 | 频率 |
| A | m | 0.15 |
| B | 60 | p |
| C | n | 0.4 |
| D | 48 | 0.2 |
(2)这次被调查的学生有多少人?并补全条形统计图.
(3)该校有1600名学生,估计该校全体学生中选择B选项的有多少人?
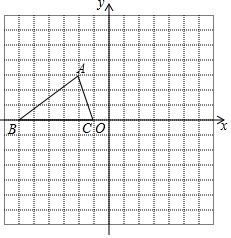 已知,如图所示的正方形网格中,每个网格的单位长度为1,△ABC的顶点均在格点上,根据所给的平面直角坐标系解答下列问题:
已知,如图所示的正方形网格中,每个网格的单位长度为1,△ABC的顶点均在格点上,根据所给的平面直角坐标系解答下列问题: 已知:抛物线y=ax2+bx-3经过点A(7,-3),与x轴正半轴交于点B(m,0)、C(6m、0)两点,与y轴交于点D.
已知:抛物线y=ax2+bx-3经过点A(7,-3),与x轴正半轴交于点B(m,0)、C(6m、0)两点,与y轴交于点D.
