题目内容
15.列方程组解应用题:某中学新建了一栋4层的教学大楼,每层楼有8间教室,进出这栋大楼共有4道门,其中两道正门大小相同,两道侧门大小也相同.安全检查中,对4道门进行了测试:当同时开启一道正门和两道侧门时,2分钟内可以通过560名学生;当同时开启一道正门和一道侧门时,4分钟内可以通过800名学生.(1)求平均每分钟一道正门和一道侧门各可以通过多少名学生?
(2)检查中发现,紧急情况下因学生拥挤,出门的效率将降低20%,安全检查规定,在紧急情况下全大楼的学生应在5分钟内通过这4道门安全撤离,假设这栋教学大楼每间教室最多有45名学生,问:建造的这4道门是否符合安全规定?请说明理由.
分析 (1)设平均每分钟一道正门可以通过x名学生,一道侧门可以通过y名学生,根据“当同时开启一道正门和两道侧门时,2分钟内可以通过560名学生;当同时开启一道正门和一道侧门时,4分钟内可以通过800名学生”,即可得出关于x、y的二元一次方程组,解之即可得出结论;
(2)求出新教学楼中的所有班级最多拥有学生数,再求出紧急情况下4道门5分钟能通过的学生数,二者比较后即可得出结论.
解答 解:(1)设平均每分钟一道正门可以通过x名学生,一道侧门可以通过y名学生,
根据题意得:$\left\{\begin{array}{l}{2x+4y=560}\\{4x+4y=800}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=120}\\{y=80}\end{array}\right.$.
答:平均每分钟一道正门可以通过120名学生,一道侧门可以通过80名学生.
(2)符合安全规定,理由如下:
新教学楼中的班级最多有学生4×8×45=1440(人),
紧急情况下,4道门5分钟最多能出学生2×(120+80)×5×(1-20%)=1600(人).
∵1440<1600,
∴建造的这4道门符合安全规定.
点评 本题考查了二元一次方程组的应用,解题的关键是:(1)找准等量关系,列出二元一次方程组;(2)根据数量关系,算出新楼所有班级最多拥有的学生数以及紧急情况下4道门5分钟能通过的学生数.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
6.若点(-2,y1)、(-1,y2)、(1,y3)在反比例函数y=$\frac{2}{x}$的图象上,则下列结论中,正确的是( )
| A. | y1>y2>y3 | B. | y2>y1>y3 | C. | y3>y1>y2 | D. | y3>y2>y1 |
4.某长方形的面积为9x2y-6xy2,若其一边长为3xy,则另一边长为( )
| A. | 3x-2y | B. | 9x-6y | C. | 3x-2 | D. | 6x-4y |
 如图,将△ABC绕点C按顺时针方向旋转64°至△A′B′C,使点A′落在BC的延长线上.则∠ACB′=52度.
如图,将△ABC绕点C按顺时针方向旋转64°至△A′B′C,使点A′落在BC的延长线上.则∠ACB′=52度.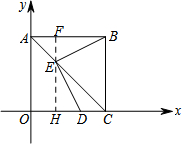 探索与发现
探索与发现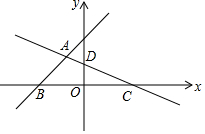 如图,在平面直角坐标系中,直线y=x+3与x轴交于点B,与直线CD交于点A(-$\frac{12}{11}$,a),点D的坐标为(0,$\frac{3}{2}$),点C在x轴上
如图,在平面直角坐标系中,直线y=x+3与x轴交于点B,与直线CD交于点A(-$\frac{12}{11}$,a),点D的坐标为(0,$\frac{3}{2}$),点C在x轴上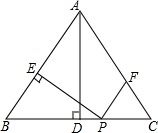 如图,在等腰△ABC中,AB=AC=5,BC=6,AD⊥BC于点D,动点P从点B出发沿BC方向以每秒5个单位的速度向终点C运动,过点P作PE⊥AB于点E,过点P作PF∥BA,交AC于点F,设点P运动的时间为t秒.若以PE所在的直线为对称轴,线段BD经轴对称变换后的图形为B'D',求当线段B'D'与线段AC有交点这段过程中,线段B'D'扫过的面积$\frac{66}{25}$.
如图,在等腰△ABC中,AB=AC=5,BC=6,AD⊥BC于点D,动点P从点B出发沿BC方向以每秒5个单位的速度向终点C运动,过点P作PE⊥AB于点E,过点P作PF∥BA,交AC于点F,设点P运动的时间为t秒.若以PE所在的直线为对称轴,线段BD经轴对称变换后的图形为B'D',求当线段B'D'与线段AC有交点这段过程中,线段B'D'扫过的面积$\frac{66}{25}$.