题目内容
5. 已知:抛物线y=ax2+bx-3经过点A(7,-3),与x轴正半轴交于点B(m,0)、C(6m、0)两点,与y轴交于点D.
已知:抛物线y=ax2+bx-3经过点A(7,-3),与x轴正半轴交于点B(m,0)、C(6m、0)两点,与y轴交于点D.(1)求m的值;
(2)求这条抛物线的表达式;
(3)点P在抛物线上,点Q在x轴上,当∠PQD=90°且PQ=2DQ时,求点P、Q的坐标.
分析 (1)先求得点D的坐标,然后设抛物线的解析式为y=a(x-m)(x-6m),把点D和点A的坐标代入可求得m的值;
(2)由6am2=-3,m=1可求得a的值,然后代入抛物线的解析式即可;
(3)过点P作PE⊥x轴,垂足为E.设点Q的坐标为(a,0)则OQ=-a,然后证明△ODQ∽△EQP,依据相似三角形的性质可求得QE=6,PE=-2a.,则P的坐标为(a+6,-2a),将点P的坐标代入抛物线的解析式可求得a的值.
解答 解:(1)当x=0时,y=-3,
∴D(0,-3).
设抛物线的解析式为y=a(x-m)(x-6m).
把点D和点A的坐标代入得:6am2=-3①,a(7-m)(7-6m)=-3②,
∴a(7-m)(7-6m)=6am2.
∵a≠0,
∴(7-m)(7-6m)=m2.
解得:m=1.
(2)∵6am2=-3,
∴a=-$\frac{3}{6{m}^{2}}$=-$\frac{1}{2}$.
将a=-$\frac{1}{2}$,m=1代入得:y=-$\frac{1}{2}$x2+$\frac{7}{2}$x-3.
∴抛物线的表达式为y=-$\frac{1}{2}$x2+$\frac{7}{2}$x-3.
(3)如图所示:过点P作PE⊥x轴,垂足为E.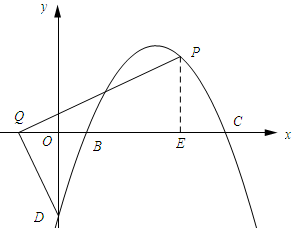
设点Q的坐标为(a,0)则OQ=-a
-∵∠DQP=90°,
∴∠PQO+∠OQD=90°.
又∵∠ODQ+∠DQO=90°,
∴∠PQE=∠ODQ.
又∵∠PEQ=∠DOQ=90°,
∴△ODQ∽△EQP.
∴$\frac{QO}{PE}$=$\frac{OD}{QE}$=$\frac{QD}{QP}$=$\frac{1}{2}$,即$\frac{-a}{3}$=$\frac{PE}{6}$=$\frac{1}{2}$,
∴QE=6,PE=-2a.
∴P的坐标为(a+6,-2a)
将点P的坐标代入抛物线的解析式得:-$\frac{1}{2}$(a+6)2+$\frac{7}{2}$(a+6)-3=-2a,整理得:a2+a=0,
解得a=-1或a=0.
当a=-1时,Q(-1,0),P(5,2);当a=0时,Q(0,0),P(6,0).
综上所述,Q(-1,0),P(5,2)或者Q(0,0),P(6,0).
点评 本题主要考查的是二次函数的综合应用,解答本题主要应用了待定系数法求二次函数的解析式、相似三角形的性质和判定,用含a的式子表示出点P的坐标是解题的关键.

| A. |  | B. |  | C. |  | D. |  |
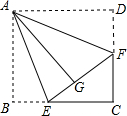 如图,在四边形纸片ABCD中,∠B=∠D=90°,点E,F分别在边BC,CD上,将AB,AD分别沿AE,AF折叠,点B,D恰好都和点G重合,∠EAF=45°.
如图,在四边形纸片ABCD中,∠B=∠D=90°,点E,F分别在边BC,CD上,将AB,AD分别沿AE,AF折叠,点B,D恰好都和点G重合,∠EAF=45°. 如图所示,AB⊥l1,AC⊥l2,则点A到直线l1的距离是线段AB的长度.
如图所示,AB⊥l1,AC⊥l2,则点A到直线l1的距离是线段AB的长度.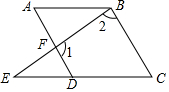 如图,已知∠A=∠C,∠1与∠2互补,求证:AB∥CD.
如图,已知∠A=∠C,∠1与∠2互补,求证:AB∥CD.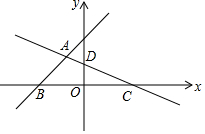 如图,在平面直角坐标系中,直线y=x+3与x轴交于点B,与直线CD交于点A(-$\frac{12}{11}$,a),点D的坐标为(0,$\frac{3}{2}$),点C在x轴上
如图,在平面直角坐标系中,直线y=x+3与x轴交于点B,与直线CD交于点A(-$\frac{12}{11}$,a),点D的坐标为(0,$\frac{3}{2}$),点C在x轴上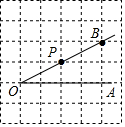 点P是∠AOB的边OB上一点.
点P是∠AOB的边OB上一点. (一)阅读
(一)阅读