题目内容
11.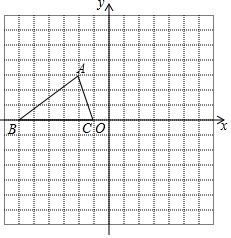 已知,如图所示的正方形网格中,每个网格的单位长度为1,△ABC的顶点均在格点上,根据所给的平面直角坐标系解答下列问题:
已知,如图所示的正方形网格中,每个网格的单位长度为1,△ABC的顶点均在格点上,根据所给的平面直角坐标系解答下列问题:(1)A点的坐标为(-2,3);B点的坐标为(-6,0);C点的坐标为(-1,0).
(2)将点A,B,C的横坐标保持不变,纵坐标分别乘以-1,分别得点A′,B′,C′,并连接A′,B′,C′得△A′B′C′,请画出△A′B′C′
(3)△A′B′C′与△ABC的位置关系是关于x轴对称.
分析 (1)根据各点在坐标系中的位置即可得出结论;
(2)把点A,B,C的横坐标保持不变,纵坐标分别乘以-1,分别得点A′,B′,C′,并连接A′,B′,C′得△A′B′C′即可;
(3)根据△A′B′C′与△ABC在坐标系中的位置即可得出结论.
解答  解:(1)A点的坐标为(-2,3);B点的坐标为(-6,0);C点的坐标为(-1,0);
解:(1)A点的坐标为(-2,3);B点的坐标为(-6,0);C点的坐标为(-1,0);
(2)如图△A′B′C′即为所求;
(3)由图可知,△A′B′C′与△ABC的位置关于x轴对称.
故答案为:关于x轴对称.
点评 本题考查的是轴对称变换,熟知关于x轴对称的点的坐标特点是解答此题的关键.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
19.盒中有3个大小相同的小球,其中2个为白色,1个为红色,每次从袋中摸1个球,然后放回搅匀再摸,在摸球实验中得到下表中部分数据.
(1)请将数据表补充完整;
(2)画出摸出红球频率的折线统计图;
(3)摸出一个红球的概率估计值是多少?
| 摸球次数 | 40 | 80 | 120 | 160 | 200 | 240 | 280 | 320 | 360 | 400 |
| 出现红色的频数 | 14 | 24 | 38 | 68 | 77 | 92 | 109 | 120 | 132 | |
| 出球红色的频率 | 35% | 32% | 35% | 34% | 33% | 34% |
(2)画出摸出红球频率的折线统计图;
(3)摸出一个红球的概率估计值是多少?
6.若点(-2,y1)、(-1,y2)、(1,y3)在反比例函数y=$\frac{2}{x}$的图象上,则下列结论中,正确的是( )
| A. | y1>y2>y3 | B. | y2>y1>y3 | C. | y3>y1>y2 | D. | y3>y2>y1 |
1.下列各式中与-2xy-x2-y2的相等的是( )
| A. | (x+y)2 | B. | -(x+y)2 | C. | (x-y)2 | D. | -(x-y)2 |
 将一副三角板中的两块直角三角尺的直角顶点C按如图所示的方式叠放在一起.
将一副三角板中的两块直角三角尺的直角顶点C按如图所示的方式叠放在一起. 如图所示,AB⊥l1,AC⊥l2,则点A到直线l1的距离是线段AB的长度.
如图所示,AB⊥l1,AC⊥l2,则点A到直线l1的距离是线段AB的长度.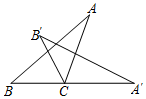 如图,将△ABC绕点C按顺时针方向旋转64°至△A′B′C,使点A′落在BC的延长线上.则∠ACB′=52度.
如图,将△ABC绕点C按顺时针方向旋转64°至△A′B′C,使点A′落在BC的延长线上.则∠ACB′=52度.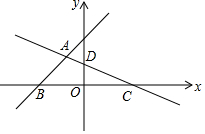 如图,在平面直角坐标系中,直线y=x+3与x轴交于点B,与直线CD交于点A(-$\frac{12}{11}$,a),点D的坐标为(0,$\frac{3}{2}$),点C在x轴上
如图,在平面直角坐标系中,直线y=x+3与x轴交于点B,与直线CD交于点A(-$\frac{12}{11}$,a),点D的坐标为(0,$\frac{3}{2}$),点C在x轴上