题目内容
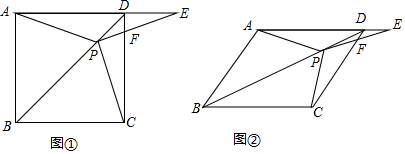
10.如图①,在正方形ABCD中,P是对角线BD上的一点,点E在AD的延长线上,且PE=PA,PE交CD于F.(1)求证:PC=PE;
(2)求∠CPE的度数;
(3)如图②,把正方形ABCD改为菱形ABCD,其它条件不变,若∠ABC=65°,则∠CPE=115度.
分析 (1)先证出△ABP≌△CBP,得PA=PC,由于PA=PE,得PC=PE;
(2)由△ABP≌△CBP,得∠BAP=∠BCP,进而得∠DAP=∠DCP,由PA=PC,得到∠DAP=∠E,∠DCP=∠E,最后∠CPF=∠EDF=90°得到结论;
(3)由△DPA≌△DPC,推出∠DAP=∠DCP,PA=PC,推出PA=PE,推出∠DAP=∠E,推出∠E=∠PCD,由∠DFE=∠CFP,推出∠CPF=∠EDF,由此即可解决问题;
解答 解:(1)证明:在正方形ABCD中,AB=BC,
∠ABP=∠CBP=45°,
在△ABP和△CBP中,
$\left\{\begin{array}{l}{AB=BC}\\{∠ABP=∠CBP}\\{PB=PB}\end{array}\right.$,
∴△ABP≌△CBP(SAS),
∴PA=PC,
∵PA=PE,
∴PC=PE;
(2)由(1)知,△ABP≌△CBP,
∴∠BAP=∠BCP,
∴∠DAP=∠DCP,
∵PA=PE,
∴∠DAP=∠E,
∴∠DCP=∠E,
∵∠CFP=∠EFD(对顶角相等),
∴180°-∠PFC-∠PCF=180°-∠DFE-∠E,
即∠CPF=∠EDF=90°;
(3)在菱形ABCD中,AD=DC,∠ADP=∠CDP,DP=DP,
∴△DPA≌△DPC,
∴∠DAP=∠DCP,PA=PC,
∵PA=PE,
∴∠DAP=∠E,
∴∠E=∠PCD,
∵∠DFE=∠CFP,
∴∠CPF=∠EDF,
∵∠ABC=∠ADC=65°,
∴∠CPE=∠EDF=180°-∠ADC=115°
故答案为115.
点评 本题考查了正方形的性质,全等三角形的判定与性质,菱形的性质,等腰三角形的判定和性质,正确寻找全等三角形的条件是解题的关键.

练习册系列答案
相关题目
19.盒中有3个大小相同的小球,其中2个为白色,1个为红色,每次从袋中摸1个球,然后放回搅匀再摸,在摸球实验中得到下表中部分数据.
(1)请将数据表补充完整;
(2)画出摸出红球频率的折线统计图;
(3)摸出一个红球的概率估计值是多少?
| 摸球次数 | 40 | 80 | 120 | 160 | 200 | 240 | 280 | 320 | 360 | 400 |
| 出现红色的频数 | 14 | 24 | 38 | 68 | 77 | 92 | 109 | 120 | 132 | |
| 出球红色的频率 | 35% | 32% | 35% | 34% | 33% | 34% |
(2)画出摸出红球频率的折线统计图;
(3)摸出一个红球的概率估计值是多少?
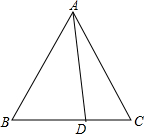 如图,在等边△ABC中,点D为BC边上一点,请你用量角器,在AC边上确定点E,使AE=CD,简述你的作法,并说明理由.
如图,在等边△ABC中,点D为BC边上一点,请你用量角器,在AC边上确定点E,使AE=CD,简述你的作法,并说明理由.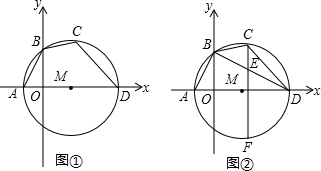
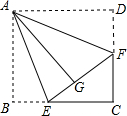 如图,在四边形纸片ABCD中,∠B=∠D=90°,点E,F分别在边BC,CD上,将AB,AD分别沿AE,AF折叠,点B,D恰好都和点G重合,∠EAF=45°.
如图,在四边形纸片ABCD中,∠B=∠D=90°,点E,F分别在边BC,CD上,将AB,AD分别沿AE,AF折叠,点B,D恰好都和点G重合,∠EAF=45°. 将一副三角板中的两块直角三角尺的直角顶点C按如图所示的方式叠放在一起.
将一副三角板中的两块直角三角尺的直角顶点C按如图所示的方式叠放在一起.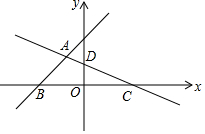 如图,在平面直角坐标系中,直线y=x+3与x轴交于点B,与直线CD交于点A(-$\frac{12}{11}$,a),点D的坐标为(0,$\frac{3}{2}$),点C在x轴上
如图,在平面直角坐标系中,直线y=x+3与x轴交于点B,与直线CD交于点A(-$\frac{12}{11}$,a),点D的坐标为(0,$\frac{3}{2}$),点C在x轴上