题目内容
9.(1)$\sqrt{48}$÷$\sqrt{3}$-$\sqrt{\frac{1}{2}}$×$\sqrt{12}$+$\sqrt{24}$(2)先化简再求值:$\frac{2x-1}{{x}^{2}-2x+1}$•(x-1),其中x=$\sqrt{2}$+1.
分析 (1)利用二次根式的乘法法则运算;
(2)先把分母因式分解,再约分得到原式=$\frac{2x-1}{x-1}$,然后把x的值代入后分母有理化即可.
解答 解:(1)原式=$\sqrt{48÷3}$-$\sqrt{\frac{1}{2}×12}$+2$\sqrt{6}$
=4-$\sqrt{6}$+2$\sqrt{6}$
=4+$\sqrt{6}$;
(2)原式=$\frac{2x-1}{(x-1)^{2}}$•(x-1)
=$\frac{2x-1}{x-1}$,
当x=$\sqrt{2}$+1时,原式=$\frac{2(\sqrt{2}+1)-1}{\sqrt{2}+1-1}$=$\frac{4+\sqrt{2}}{2}$.
点评 本题考查了二次根式的混合运算:先把各二次根式化简为最简二次根式,然后进行二次根式的乘除运算,再合并即可.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
19.盒中有3个大小相同的小球,其中2个为白色,1个为红色,每次从袋中摸1个球,然后放回搅匀再摸,在摸球实验中得到下表中部分数据.
(1)请将数据表补充完整;
(2)画出摸出红球频率的折线统计图;
(3)摸出一个红球的概率估计值是多少?
| 摸球次数 | 40 | 80 | 120 | 160 | 200 | 240 | 280 | 320 | 360 | 400 |
| 出现红色的频数 | 14 | 24 | 38 | 68 | 77 | 92 | 109 | 120 | 132 | |
| 出球红色的频率 | 35% | 32% | 35% | 34% | 33% | 34% |
(2)画出摸出红球频率的折线统计图;
(3)摸出一个红球的概率估计值是多少?
4.某长方形的面积为9x2y-6xy2,若其一边长为3xy,则另一边长为( )
| A. | 3x-2y | B. | 9x-6y | C. | 3x-2 | D. | 6x-4y |
14.下列图形不可由平移得到的是( )
| A. |  | B. |  | C. |  | D. |  |
1.下列各式中与-2xy-x2-y2的相等的是( )
| A. | (x+y)2 | B. | -(x+y)2 | C. | (x-y)2 | D. | -(x-y)2 |
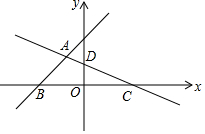 如图,在平面直角坐标系中,直线y=x+3与x轴交于点B,与直线CD交于点A(-$\frac{12}{11}$,a),点D的坐标为(0,$\frac{3}{2}$),点C在x轴上
如图,在平面直角坐标系中,直线y=x+3与x轴交于点B,与直线CD交于点A(-$\frac{12}{11}$,a),点D的坐标为(0,$\frac{3}{2}$),点C在x轴上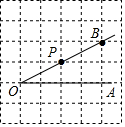 点P是∠AOB的边OB上一点.
点P是∠AOB的边OB上一点.