题目内容
如图，△ABC是等边三角形，D是BC上一点，△ABD经过逆时针旋转后到达△ACE的位置，M是AB的中点，那么经过旋转后，点M转到（ ）| A、AE的中点 |
| B、BC的中点 |
| C、DC的中点 |
| D、AC的中点 |
考点：旋转的性质
专题：常规题型
分析：先等边三角形的性质得到AB=AC，再根据旋转的性质得AB与AC为对应边，由于M是AB的中点，则M点的对应点为AC的中点．
解答：解：∵△ABC是等边三角形，
∴AB=AC，
∵△ABD经过逆时针旋转后到达△ACE的位置，
∴AB与AC为对应边，
∵M是AB的中点，
∴旋转后，点M转到AC的中点．
故选D．
∴AB=AC，
∵△ABD经过逆时针旋转后到达△ACE的位置，
∴AB与AC为对应边，
∵M是AB的中点，
∴旋转后，点M转到AC的中点．
故选D．
点评：本题考查了旋转的性质：旋转前后两图形全等；对应点到旋转中心的距离相等；对应点与旋转中心的连线段的夹角等于旋转角．也考查了等边三角形的性质．
练习册系列答案
相关题目
如图，在△ABC中，分别以AC，BC为边作等边△ACD和等边△BCE．设△ACD、△BCE、△ABC的面积分别是S1、S2、S3，现有如下结论：使用同一种规格的下列地砖，不能进行平面镶嵌的是（ ）
| A、正三角形地砖 |
| B、正四边形地砖 |
| C、正五边形地砖 |
| D、正六边形地砖 |
不等式1-2x≥
x的解集是（ ）
| 1 |
| 2 |
A、x≥
| ||
B、x≤
| ||
C、x≥-
| ||
D、x≤-
|
实数m，n满足mn=1，记P=
+
，Q=
+
，则P、Q的大小关系为（ ）
| 1 |
| 1+m |
| 1 |
| 1+n |
| m |
| 1+m |
| n |
| 1+n |
| A、P＞Q | B、P=Q |
| C、P＜Q | D、不确定 |
如果0＜x＜1，那么x，
，
，x2中，值最小的是（ ）
| 1 |
| x |
| x |
| A、x | ||
B、
| ||
C、
| ||
| D、x2 |
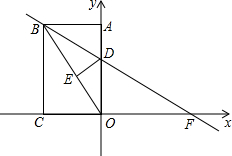如图，矩形ABCO中，点C在x轴上，点A在y轴上，点B的坐标是（-12，16），矩形ABCO沿直线BD折叠，使得点A落在对角线OB上的点E处，折痕与OA、x轴分别交于点D、F．
如图，∠B=∠ACD=90°，AD=13，CD=12，BC=3，则AB的长是多少？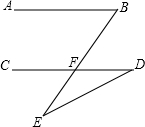
如图，已知：∠B=∠D+∠E，试说明：AB∥CD．