题目内容
16．
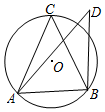如图，锐角△ABC内接于⊙O，点D在⊙O外（与点C在AB同侧），∠ABD=90°，下列结论：①sinC＞sinD；②cosC＞cosD；③tanC＞tanD，正确的结论为（ ）| A． | ①② | B． | ②③ | C． | ①②③ | D． | ①③ |
分析 首先设BD交⊙O于点E，连接AE，由圆周角定理，易得∠C＞∠D，继而求得答案．
解答 
解：设BD交⊙O于点E，连接AE，
∵∠C=∠AEB，∠AEB＞∠D，
∴∠C＞∠D，
∴sin∠C＞sin∠D；cos∠C＜cos∠D；tan∠C＞tan∠D，
∴正确的结论有：①③．
故选D．
点评 此题考查的是三角形的外接圆与外心、圆周角定理以及三角函数的性质，注意准确作出辅助线是解此题的关键．
练习册系列答案
相关题目
6．下列计算正确的是（ ）
| A． | xy•xy=2xy | B． | 3$\sqrt{x}$-$\sqrt{x}$=3（x≥0） | C． | （2x）3=2x3 | D． | $\sqrt{x}$•$\sqrt{y}$=$\sqrt{xy}$（x≥0，y≥0） |
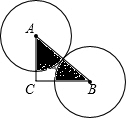如图，Rt△ABC中，∠C=90°，AC=4，BC=4$\sqrt{3}$，两等圆⊙A，⊙B外切，那么图中两个扇形（即阴影部分）的面积之和为（ ）
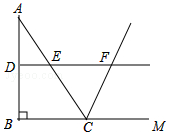如图，在△ABC中，∠ABC=90°，∠A=30°，BC=4．若DE是△ABC的中位线，延长DE交∠ACM的平分线于点F，则DF的长为（ ）
1．将点A（3，-2）绕原点逆时针旋转90°得到点B，则点B的坐标为（ ）
| A． | （2，3） | B． | （2，-3） | C． | （-3，2） | D． | （-3，-2） |
8．下列各数中，最小的数是（ ）
| A． | -3 | B． | |-2| | C． | （-3）2 | D． | 2×10-5 |
5．
如图，已知AB是⊙O的直径，∠D=36°，则∠CAB的度数为（ ）
如图，已知AB是⊙O的直径，∠D=36°，则∠CAB的度数为（ ）| A． | 18° | B． | 36° | C． | 54° | D． | 72° |
如图，在网格中，小正方形的边长均为1，点A，B，C都在格点上，则sin∠ABC=$\frac{\sqrt{5}}{5}$．