题目内容
6. 如图,在网格中,小正方形的边长均为1,点A,B,C都在格点上,则sin∠ABC=$\frac{\sqrt{5}}{5}$.
如图,在网格中,小正方形的边长均为1,点A,B,C都在格点上,则sin∠ABC=$\frac{\sqrt{5}}{5}$.
分析 由小正方形边长为1,利用勾股定理分别求出AB2,AC2,BC2,再利用勾股定理的逆定理证明△ABC是直角三角形,然后根据正切函数定义即可求出tan∠BAC的值.
解答 解:∵小正方形边长为1,
∴AB2=8,bC2=10,AC2=2;
∴AB2+BC2=AC2,
∴△ABC是直角三角形,且∠ABC=90°,
∴sin∠ABC=$\frac{AC}{BC}$=$\frac{\sqrt{2}}{\sqrt{10}}$=$\frac{\sqrt{5}}{5}$.
故答案为$\frac{\sqrt{5}}{5}$.
点评 此题主要考查勾股定理及其逆定理,锐角三角函数的定义等知识点,此题难易程度适中,得到∠ABC=90°是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.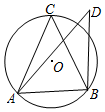 如图,锐角△ABC内接于⊙O,点D在⊙O外(与点C在AB同侧),∠ABD=90°,下列结论:①sinC>sinD;②cosC>cosD;③tanC>tanD,正确的结论为( )
如图,锐角△ABC内接于⊙O,点D在⊙O外(与点C在AB同侧),∠ABD=90°,下列结论:①sinC>sinD;②cosC>cosD;③tanC>tanD,正确的结论为( )
 如图,锐角△ABC内接于⊙O,点D在⊙O外(与点C在AB同侧),∠ABD=90°,下列结论:①sinC>sinD;②cosC>cosD;③tanC>tanD,正确的结论为( )
如图,锐角△ABC内接于⊙O,点D在⊙O外(与点C在AB同侧),∠ABD=90°,下列结论:①sinC>sinD;②cosC>cosD;③tanC>tanD,正确的结论为( )| A. | ①② | B. | ②③ | C. | ①②③ | D. | ①③ |
17.定义一种运算“◎”,规定x◎y=ax-by,其中a、b为常数,且2◎3=6,3◎2=8,则a+b的值是( )
| A. | 2 | B. | -2 | C. | $\frac{16}{3}$ | D. | 4 |
14.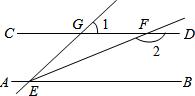 如图,已知直线AB∥CD,∠GEB的平分线EF交CD于点F,∠1=60°,则∠2等于( )
如图,已知直线AB∥CD,∠GEB的平分线EF交CD于点F,∠1=60°,则∠2等于( )
 如图,已知直线AB∥CD,∠GEB的平分线EF交CD于点F,∠1=60°,则∠2等于( )
如图,已知直线AB∥CD,∠GEB的平分线EF交CD于点F,∠1=60°,则∠2等于( )| A. | 130° | B. | 140° | C. | 150° | D. | 160° |
1.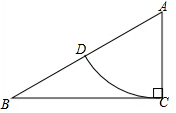 如图,在△ABC中,∠ACB=90°,AC=1,AB=2,以A为圆心,AC长为半径画弧,交AB于D,则扇形CAD的周长是(结果保留π)( )
如图,在△ABC中,∠ACB=90°,AC=1,AB=2,以A为圆心,AC长为半径画弧,交AB于D,则扇形CAD的周长是(结果保留π)( )
 如图,在△ABC中,∠ACB=90°,AC=1,AB=2,以A为圆心,AC长为半径画弧,交AB于D,则扇形CAD的周长是(结果保留π)( )
如图,在△ABC中,∠ACB=90°,AC=1,AB=2,以A为圆心,AC长为半径画弧,交AB于D,则扇形CAD的周长是(结果保留π)( )| A. | 1+π | B. | 2+$\frac{π}{2}$ | C. | 1$+\frac{2π}{3}$ | D. | 2+$\frac{π}{3}$ |

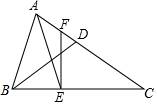 如图,△ABC中,D在AC边上,BD=CD,E在BC边上,AE=AB,过点E作EF⊥BC,交AC于F.若AD=5,CE=8,则EF的长为6.
如图,△ABC中,D在AC边上,BD=CD,E在BC边上,AE=AB,过点E作EF⊥BC,交AC于F.若AD=5,CE=8,则EF的长为6.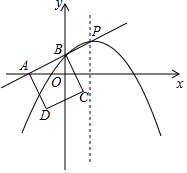 如图,在平面直角坐标系中,直线y=kx+b分别与x轴、y轴交于A、B两点,过点B的抛物线y=-$\frac{1}{4}$(x-2)2+m的顶点P在这条直线上,以AB为边向下方做正方形ABCD.
如图,在平面直角坐标系中,直线y=kx+b分别与x轴、y轴交于A、B两点,过点B的抛物线y=-$\frac{1}{4}$(x-2)2+m的顶点P在这条直线上,以AB为边向下方做正方形ABCD.