题目内容
4.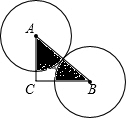 如图,Rt△ABC中,∠C=90°,AC=4,BC=4$\sqrt{3}$,两等圆⊙A,⊙B外切,那么图中两个扇形(即阴影部分)的面积之和为( )
如图,Rt△ABC中,∠C=90°,AC=4,BC=4$\sqrt{3}$,两等圆⊙A,⊙B外切,那么图中两个扇形(即阴影部分)的面积之和为( )| A. | 2π | B. | 4π | C. | 6π | D. | 8π |
分析 先依据勾股定理求得AB的长,从而可求得两圆的半径为4,然后由∠A+∠B=90°可知阴影部分的面积等于一个圆的面积的$\frac{1}{4}$.
解答 解:在△ABC中,依据勾股定理可知AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=8.
∵两等圆⊙A,⊙B外切,
∴两圆的半径均为4.
∵∠A+∠B=90°,
∴阴影部分的面积=$\frac{90π×{4}^{2}}{360}$=4π.
故选:B.
点评 本题主要考查的是相切两圆的性质、勾股定理的应用、扇形面积的计算,求得两个扇形的半径和圆心角之和是解题的关键.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
14.太阳的表面温度大约有6000℃,而太阳中心的温度达到了1920万℃,其中“1920万”用科学记数法可将表示为( )
| A. | 1.92×103 | B. | 1.92×107 | C. | 19.2×102 | D. | 0.192×108 |
15.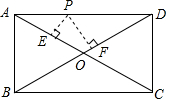 如图,P是矩形ABCD的边AD上一个动点,PE⊥AC于E,PF⊥BD于F,当P从A向D运动(P与A,D不重合),则PE+PF的值( )
如图,P是矩形ABCD的边AD上一个动点,PE⊥AC于E,PF⊥BD于F,当P从A向D运动(P与A,D不重合),则PE+PF的值( )
 如图,P是矩形ABCD的边AD上一个动点,PE⊥AC于E,PF⊥BD于F,当P从A向D运动(P与A,D不重合),则PE+PF的值( )
如图,P是矩形ABCD的边AD上一个动点,PE⊥AC于E,PF⊥BD于F,当P从A向D运动(P与A,D不重合),则PE+PF的值( )| A. | 增大 | B. | 减小 | C. | 不变 | D. | 先增大再减小 |
9.据河南省发改委发布消息,2016年全省固定资产投资继续保持持续稳定增长,全年完成39753亿元,总量居全国第3位.将数据39753亿用科学记数法表示为( )
| A. | 3.9753×109 | B. | 0.39753×1010 | C. | 39.753×1011 | D. | 3.9753×1012 |
16.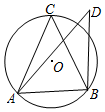 如图,锐角△ABC内接于⊙O,点D在⊙O外(与点C在AB同侧),∠ABD=90°,下列结论:①sinC>sinD;②cosC>cosD;③tanC>tanD,正确的结论为( )
如图,锐角△ABC内接于⊙O,点D在⊙O外(与点C在AB同侧),∠ABD=90°,下列结论:①sinC>sinD;②cosC>cosD;③tanC>tanD,正确的结论为( )
 如图,锐角△ABC内接于⊙O,点D在⊙O外(与点C在AB同侧),∠ABD=90°,下列结论:①sinC>sinD;②cosC>cosD;③tanC>tanD,正确的结论为( )
如图,锐角△ABC内接于⊙O,点D在⊙O外(与点C在AB同侧),∠ABD=90°,下列结论:①sinC>sinD;②cosC>cosD;③tanC>tanD,正确的结论为( )| A. | ①② | B. | ②③ | C. | ①②③ | D. | ①③ |
13.下列各式计算正确的是( )
| A. | a2+a2=a4 | B. | (-2x)3=-8x3 | C. | a3•a4=a12 | D. | (x-3)2=x2-9 |
14.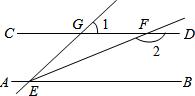 如图,已知直线AB∥CD,∠GEB的平分线EF交CD于点F,∠1=60°,则∠2等于( )
如图,已知直线AB∥CD,∠GEB的平分线EF交CD于点F,∠1=60°,则∠2等于( )
 如图,已知直线AB∥CD,∠GEB的平分线EF交CD于点F,∠1=60°,则∠2等于( )
如图,已知直线AB∥CD,∠GEB的平分线EF交CD于点F,∠1=60°,则∠2等于( )| A. | 130° | B. | 140° | C. | 150° | D. | 160° |







