题目内容
1.将点A(3,-2)绕原点逆时针旋转90°得到点B,则点B的坐标为( )| A. | (2,3) | B. | (2,-3) | C. | (-3,2) | D. | (-3,-2) |
分析 分别过A、B作x轴的垂线,垂足分别为C、D,可证明△AOC≌△OBD,可求得BD和OB的长,则可求得B点坐标.
解答  解:如图,分别过A、B作y轴的垂线,垂足分别为C、D,
解:如图,分别过A、B作y轴的垂线,垂足分别为C、D,
∵A(3,-2),
∴OC=2,AC=3,
∵把点A(3,-2)逆时针旋转90°得到点B,
∴OA=OB,且∠AOB=90°,
∴∠BOD+∠AOC=∠AOC+∠CAO=90°,
∴∠BOD=∠CAO,
在△AOC和△OBD中,$\left\{\begin{array}{l}{∠ACO=∠BDO}&{\;}\\{∠OAC=∠BOD}&{\;}\\{OA=OB}&{\;}\end{array}\right.$,
∴△AOC≌△OBD(AAS),
∴OD=AC=3,BD=OC=2,
∴B(2,3),
故选:A.
点评 本题主要考查旋转的性质,全等三角形的判定与性质;构造三角形全等求得线段的长度是解题的关键,注意旋转前后对应线段相等.

练习册系列答案
相关题目
11.若正整数按如图所示的规律排列,则第8行第5列的数字是( )


| A. | 64 | B. | 56 | C. | 58 | D. | 60 |
9.据河南省发改委发布消息,2016年全省固定资产投资继续保持持续稳定增长,全年完成39753亿元,总量居全国第3位.将数据39753亿用科学记数法表示为( )
| A. | 3.9753×109 | B. | 0.39753×1010 | C. | 39.753×1011 | D. | 3.9753×1012 |
16.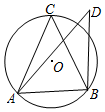 如图,锐角△ABC内接于⊙O,点D在⊙O外(与点C在AB同侧),∠ABD=90°,下列结论:①sinC>sinD;②cosC>cosD;③tanC>tanD,正确的结论为( )
如图,锐角△ABC内接于⊙O,点D在⊙O外(与点C在AB同侧),∠ABD=90°,下列结论:①sinC>sinD;②cosC>cosD;③tanC>tanD,正确的结论为( )
 如图,锐角△ABC内接于⊙O,点D在⊙O外(与点C在AB同侧),∠ABD=90°,下列结论:①sinC>sinD;②cosC>cosD;③tanC>tanD,正确的结论为( )
如图,锐角△ABC内接于⊙O,点D在⊙O外(与点C在AB同侧),∠ABD=90°,下列结论:①sinC>sinD;②cosC>cosD;③tanC>tanD,正确的结论为( )| A. | ①② | B. | ②③ | C. | ①②③ | D. | ①③ |
13.下列各式计算正确的是( )
| A. | a2+a2=a4 | B. | (-2x)3=-8x3 | C. | a3•a4=a12 | D. | (x-3)2=x2-9 |
10.下列运算正确的是( )
| A. | a2+a2=a4 | B. | (ab)2=ab2 | C. | a6÷a2=a3 | D. | (2a2)3=8a6 |




 如图,在△ABC中,中线BE,CD相交于点O,连接DE,下列结论:
如图,在△ABC中,中线BE,CD相交于点O,连接DE,下列结论: