题目内容
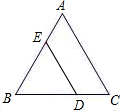 如图,△ABC是等边三角形,点D在BC边上,DE∥AC.求证:△BDE是等边三角形.
如图,△ABC是等边三角形,点D在BC边上,DE∥AC.求证:△BDE是等边三角形.考点:等边三角形的判定与性质
专题:证明题
分析:根据等边三角形ABC的性质推知∠A=∠B=∠C=60°;然后由“两直线平行,同位角相等”推知∠BDE=∠A=60°,∠BED=∠B=60°,从而证得∠B=∠BDE=∠BED=60°,所以△BDE是等边三角形.
解答:证明:∵△ABC是等边三角形,
∴∠A=∠B=∠C=60°;
又∵DE∥AC,
∴∠BDE=∠A=60°,∠BED=∠C=60°,
∴∠B=∠BDE=∠BED=60°,
∴△BDE是等边三角形.
∴∠A=∠B=∠C=60°;
又∵DE∥AC,
∴∠BDE=∠A=60°,∠BED=∠C=60°,
∴∠B=∠BDE=∠BED=60°,
∴△BDE是等边三角形.
点评:本题考查了等边三角形的判定与性质、平行线的性质.等边三角形的三个内角都是60°.

练习册系列答案
相关题目
下列说法中正确的是( )
| A、不确定事件发生的概率是不确定的 |
| B、事件发生的概率可以等于事件不发生的概率 |
| C、事件发生的概率不可能等于0 |
| D、抛掷一只均匀的骰子两次,朝上一面的点数之和一定大于2 |
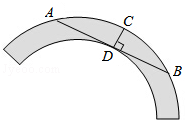 如图是一个古代车轮的碎片,小明为求其外圆半径,连结外圆上的两点A、B,并使AB与车轮内圆相切于点D,作CD⊥AB交外圆于点C.测得CD=10cm,AB=60cm,求这个车轮的外圆半径长.
如图是一个古代车轮的碎片,小明为求其外圆半径,连结外圆上的两点A、B,并使AB与车轮内圆相切于点D,作CD⊥AB交外圆于点C.测得CD=10cm,AB=60cm,求这个车轮的外圆半径长.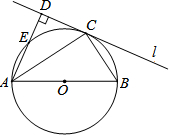 如图,AB为⊙O的直径,直线l与⊙O相切于点C,过点A作AD⊥l于点D,交⊙O于点E.
如图,AB为⊙O的直径,直线l与⊙O相切于点C,过点A作AD⊥l于点D,交⊙O于点E.
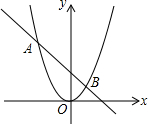 如图,抛物线y=ax2与直线y=bx+c的两个交点坐标分别为A(-2,4),B(1,1),则关于x的方程ax2-bx-c=0的解为
如图,抛物线y=ax2与直线y=bx+c的两个交点坐标分别为A(-2,4),B(1,1),则关于x的方程ax2-bx-c=0的解为 如图所示,同位角的个数是
如图所示,同位角的个数是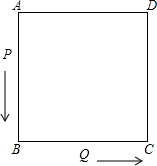 点P、Q在边长为10cm的正方形边上运动,按A→B→C→D→A→…方向,点P从A以70cm/min的速度,点Q从B以50cm/min的速度运动,如图所示,等点P第2005次追上点Q时,是在正方形的
点P、Q在边长为10cm的正方形边上运动,按A→B→C→D→A→…方向,点P从A以70cm/min的速度,点Q从B以50cm/min的速度运动,如图所示,等点P第2005次追上点Q时,是在正方形的