题目内容
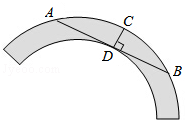 如图是一个古代车轮的碎片,小明为求其外圆半径,连结外圆上的两点A、B,并使AB与车轮内圆相切于点D,作CD⊥AB交外圆于点C.测得CD=10cm,AB=60cm,求这个车轮的外圆半径长.
如图是一个古代车轮的碎片,小明为求其外圆半径,连结外圆上的两点A、B,并使AB与车轮内圆相切于点D,作CD⊥AB交外圆于点C.测得CD=10cm,AB=60cm,求这个车轮的外圆半径长.考点:垂径定理的应用,勾股定理
专题:
分析:根据垂径定理求得AD=30cm,然后根据勾股定理即可求得半径.
解答:解: 如图,设点O为外圆的圆心,连接OA和OC,
如图,设点O为外圆的圆心,连接OA和OC,
∵CD=10cm,AB=60cm,
∵CD⊥AB,
∴OC⊥AB,
∴AD=
AB=30cm,
∴设半径为r,则OD=r-10,
根据题意得:r2=(r-10)2+302,
解得:r=50.
∴这个车轮的外圆半径长为50.
 如图,设点O为外圆的圆心,连接OA和OC,
如图,设点O为外圆的圆心,连接OA和OC,∵CD=10cm,AB=60cm,
∵CD⊥AB,
∴OC⊥AB,
∴AD=
| 1 |
| 2 |
∴设半径为r,则OD=r-10,
根据题意得:r2=(r-10)2+302,
解得:r=50.
∴这个车轮的外圆半径长为50.
点评:本题考查了垂径定理的应用以及勾股定理的应用,作出辅助线构建直角三角形是本题的关键.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
 如图,已知∠A=∠F,∠C=∠D,问BD与CE平行吗?并说明理由.
如图,已知∠A=∠F,∠C=∠D,问BD与CE平行吗?并说明理由. 如图,大半圆的弦AB平行于直径CD,且与小半圆相切,已知AB=16cm,求图中阴影部分的面积.
如图,大半圆的弦AB平行于直径CD,且与小半圆相切,已知AB=16cm,求图中阴影部分的面积.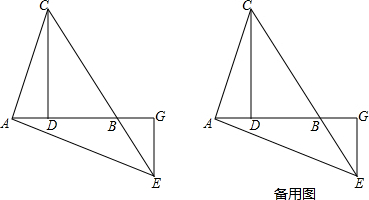
 如图,∠AOB=90°,以O为顶点的锐角共有
如图,∠AOB=90°,以O为顶点的锐角共有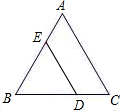 如图,△ABC是等边三角形,点D在BC边上,DE∥AC.求证:△BDE是等边三角形.
如图,△ABC是等边三角形,点D在BC边上,DE∥AC.求证:△BDE是等边三角形. (1)如图1,D是线段BC的中点,三角形ABC的面积与三角形ABD的面积比为
(1)如图1,D是线段BC的中点,三角形ABC的面积与三角形ABD的面积比为