题目内容
下列说法中正确的是( )
| A、不确定事件发生的概率是不确定的 |
| B、事件发生的概率可以等于事件不发生的概率 |
| C、事件发生的概率不可能等于0 |
| D、抛掷一只均匀的骰子两次,朝上一面的点数之和一定大于2 |
考点:概率的意义
专题:
分析:大量反复试验时,某事件发生的频率会稳定在某个常数的附近,这个常数就叫做事件概率的估计值,而不是一种必然的结果,可得答案.
解答:解:A、用频率估计概率,不确定事件的概率是确定的,故A错误;
B、抛掷硬币,正面朝上的概率等于反面朝上的概率,故B正确;
C、不可能发生事件的概率是0,故C错误;
D、抛掷一枚均匀的骰子两次,朝上一面的点数之和可能等于2,故D错误,
故选:B.
B、抛掷硬币,正面朝上的概率等于反面朝上的概率,故B正确;
C、不可能发生事件的概率是0,故C错误;
D、抛掷一枚均匀的骰子两次,朝上一面的点数之和可能等于2,故D错误,
故选:B.
点评:考查利用频率估计概率.大量反复试验下频率稳定值即概率.注意随机事件发生的概率在0和1之间.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
如果将抛物线y=x2+2先向下平移1个单位,再向左平移1个单位,那么所得新抛物线的解析式是( )
| A、y=(x-1)2+2 |
| B、y=(x+1)2+1 |
| C、y=x2+1 |
| D、y=(x+1)2-1 |
已知△ABC∽△DEF,相似比为1:2,△ABC的周长为4,则△DEF的周长为( )
| A、2 | B、4 | C、8 | D、16 |
已知点A(x1,y1),B(x2,y2)是反比例函数y=-
的图象上的两点,若x1<0<x2,则下列结论正确的是( )
| 3 |
| x |
| A、y1<0<y2 |
| B、y2<0<y1 |
| C、y1<y2<0 |
| D、y2<y1<0 |
下列合并同类项正确的是( )
| A、-5a3+2a3=-3 | ||
| B、ab+2ab=3a2b2 | ||
C、0.75m2n-
| ||
| D、4a2b-4ab=0 |
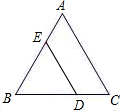 如图,△ABC是等边三角形,点D在BC边上,DE∥AC.求证:△BDE是等边三角形.
如图,△ABC是等边三角形,点D在BC边上,DE∥AC.求证:△BDE是等边三角形.