题目内容
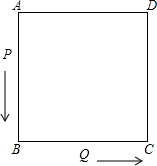 点P、Q在边长为10cm的正方形边上运动,按A→B→C→D→A→…方向,点P从A以70cm/min的速度,点Q从B以50cm/min的速度运动,如图所示,等点P第2005次追上点Q时,是在正方形的
点P、Q在边长为10cm的正方形边上运动,按A→B→C→D→A→…方向,点P从A以70cm/min的速度,点Q从B以50cm/min的速度运动,如图所示,等点P第2005次追上点Q时,是在正方形的考点:一元一次方程的应用
专题:几何动点问题
分析:设点Px分钟后第2005次追上点Q,根据点P第2005次追上点Q时点P比点Q多走了10×4×2005cm,可得出方程,求出时间后,计算点P所走的路程,继而可判断在正方形的哪一点上.
解答:解:设点Px分钟后第2005次追上点Q,由题意得
70x-50x=10×4×2005,
解得:x=4010,
而70×4010=280700(cm),
280700÷40=7017…20(cm),
即等点P第2005次追上点Q时,是在正方形的C点.
故答案为:C.
70x-50x=10×4×2005,
解得:x=4010,
而70×4010=280700(cm),
280700÷40=7017…20(cm),
即等点P第2005次追上点Q时,是在正方形的C点.
故答案为:C.
点评:本题考查了一元一次方程的应用,完成本题要注意通过所行路程及正方形的周长正确判断追上时在正方形的哪一点上.

练习册系列答案
相关题目
有理数6的相反数是( )
| A、-6 | ||
| B、6 | ||
C、
| ||
D、-
|
下列合并同类项正确的是( )
| A、-5a3+2a3=-3 | ||
| B、ab+2ab=3a2b2 | ||
C、0.75m2n-
| ||
| D、4a2b-4ab=0 |
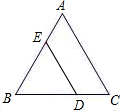 如图,△ABC是等边三角形,点D在BC边上,DE∥AC.求证:△BDE是等边三角形.
如图,△ABC是等边三角形,点D在BC边上,DE∥AC.求证:△BDE是等边三角形. (1)如图1,D是线段BC的中点,三角形ABC的面积与三角形ABD的面积比为
(1)如图1,D是线段BC的中点,三角形ABC的面积与三角形ABD的面积比为 如图,已知AB∥CD,∠1:∠2:∠3=1:2:3,则∠EBA的度数为
如图,已知AB∥CD,∠1:∠2:∠3=1:2:3,则∠EBA的度数为



 2014年3月8日凌晨,马来西亚航空公司MH370航班与总部失去联系,我国随即针对该航班展开了大规模搜救行动,我国的侦察机和搜救船在某海域同时沿同一方向配合搜寻(如图13).在距海面900米的高空A处,侦察机测得搜救船在俯角为30°的海面C处,当侦察机以150
2014年3月8日凌晨,马来西亚航空公司MH370航班与总部失去联系,我国随即针对该航班展开了大规模搜救行动,我国的侦察机和搜救船在某海域同时沿同一方向配合搜寻(如图13).在距海面900米的高空A处,侦察机测得搜救船在俯角为30°的海面C处,当侦察机以150