题目内容
如图,在平面直角坐标系中,点A坐标为(0,m+4),点B坐标为(m+3,m),且m是方程
+2m=1的解.
(1)请求出A、B两点的坐标;
(2)点C在第一象限内,AC∥x轴,将线段AB进行适当的平移得到线段AD,点A的对应点为点D,点B的对应点为点C,连接AD,若三角形ACD的面积为12,求线段AC的长.
(3)在(2)的条件下,连接OD,P为y轴上一个动点,若使三角形PAB的面积等于三角形AOD的面积,求此时点P的坐标.

| 3m+9 |
| 2 |
(1)请求出A、B两点的坐标;
(2)点C在第一象限内,AC∥x轴,将线段AB进行适当的平移得到线段AD,点A的对应点为点D,点B的对应点为点C,连接AD,若三角形ACD的面积为12,求线段AC的长.
(3)在(2)的条件下,连接OD,P为y轴上一个动点,若使三角形PAB的面积等于三角形AOD的面积,求此时点P的坐标.

考点:坐标与图形性质,解一元一次方程,三角形的面积,坐标与图形变化-平移
专题:计算题
分析:(1)通过解一元一次方程求出m,从而得到点A和B的坐标;
(2)先利用AC∥x轴得到C点的纵坐标为3,说明点B向上平移了4个单位,则点A向上平移了4个单位,于是得到点D到AC的距离为4,则可根据三角形面积公式计算出AC的长;
(3)先确定C点坐标为(6,3),根据点平移的规律得到点B向上平移4个单位,再向右平移4个单位得到点C,所以点A向上平移4个单位,再向右平移4个单位得到点D,即D(4,7),再计算出S△AOD=6,然后设P点坐标为(0,t),利用三角形面积公式得到
•|t-3|•2=6,再求出t即可得到点P的坐标.
(2)先利用AC∥x轴得到C点的纵坐标为3,说明点B向上平移了4个单位,则点A向上平移了4个单位,于是得到点D到AC的距离为4,则可根据三角形面积公式计算出AC的长;
(3)先确定C点坐标为(6,3),根据点平移的规律得到点B向上平移4个单位,再向右平移4个单位得到点C,所以点A向上平移4个单位,再向右平移4个单位得到点D,即D(4,7),再计算出S△AOD=6,然后设P点坐标为(0,t),利用三角形面积公式得到
| 1 |
| 2 |
解答:解:(1)解方程
+2m=1得x=-1,
所以点A坐标为(0,3),点B坐标为(2,-1);
(2)∵AC∥x轴,
∴C点的纵坐标为3,
∵点B的对应点为点C,
而B(2,-1),
∴点B向上平移了4个单位,
∴点A向上平移了4个单位,
∴点D到AC的距离为4,
∵
×4×AC=12,
∴AC=6;
(3)∵AC=6,AC∥x轴,
∴C点坐标为(6,3),
∴点B向上平移4个单位,再向右平移4个单位得到点C,
∴点A向上平移4个单位,再向右平移4个单位得到点D,即D(4,7),
∴S△AOD=
×3×4=6,
设P点坐标为(0,t),
则
•|t-3|•2=6,解得t=-3或t=9,
∴点P的坐标为(0,-3)或(0,-9).
| 3m+9 |
| 2 |
所以点A坐标为(0,3),点B坐标为(2,-1);
(2)∵AC∥x轴,
∴C点的纵坐标为3,
∵点B的对应点为点C,
而B(2,-1),
∴点B向上平移了4个单位,
∴点A向上平移了4个单位,
∴点D到AC的距离为4,
∵
| 1 |
| 2 |
∴AC=6;
(3)∵AC=6,AC∥x轴,
∴C点坐标为(6,3),
∴点B向上平移4个单位,再向右平移4个单位得到点C,
∴点A向上平移4个单位,再向右平移4个单位得到点D,即D(4,7),
∴S△AOD=
| 1 |
| 2 |
设P点坐标为(0,t),
则
| 1 |
| 2 |
∴点P的坐标为(0,-3)或(0,-9).
点评:本题考查了坐标与图形性质:利用点的坐标计算相应线段的长和判断线段与坐标轴的位置关系;记住平面直角坐标系中各特殊位置点的坐标特征.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
关于圆有如下的命题:
①平分弦的直径垂直于弦;②不在同一条直线上的三点确定一个圆;③在一个圆中,90°的圆周角所对的弦是直径;④相等的圆心角所对的弧相等.
其中命题正确的是( )
①平分弦的直径垂直于弦;②不在同一条直线上的三点确定一个圆;③在一个圆中,90°的圆周角所对的弦是直径;④相等的圆心角所对的弧相等.
其中命题正确的是( )
| A、①② | B、②③ | C、③④ | D、①④ |
在Rt△ABC中,∠C=90°,BC=3,AB=5,则cosB的值等于( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
有理数6的相反数是( )
| A、-6 | ||
| B、6 | ||
C、
| ||
D、-
|
 如图,∠AOB=90°,以O为顶点的锐角共有
如图,∠AOB=90°,以O为顶点的锐角共有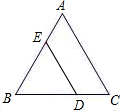 如图,△ABC是等边三角形,点D在BC边上,DE∥AC.求证:△BDE是等边三角形.
如图,△ABC是等边三角形,点D在BC边上,DE∥AC.求证:△BDE是等边三角形.