Question

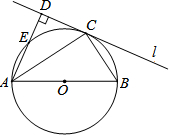如图，AB为⊙O的直径，直线l与⊙O相切于点C，过点A作AD⊥l于点D，交⊙O于点E．
（1）求证：∠CAD=∠BAC；
（2）若sin∠BAC=

3

5

，BC=6，求DE的长．

Answer 1

考点：切线的性质

专题：

分析：（1）连接BC，OC，根据圆周角定理和弦切角定理可证得∠CAD=∠BAC；
（2）过点B作BF⊥l于点F，连接BE，先证得四边形DEBF是矩形，得出DE=BF，根据切线的性质求得∠BCF=∠BAC，然后通过解直角三角形得出sin∠BCF=

BF

BC

=sin∠BAC=

3

5

，即可求得BF，从而求得DE．

解答：（1）证明：连接OC，

∵CD为⊙O的切线，
∴OC⊥CD，
∵AD⊥CD，
∴OC∥AD，
∴∠CAD=∠ACO．
又∵OC=OA，
∴∠ACO=∠OAC，
∴∠CAD=∠OAC，
即∠CAD=∠BAC．                  
（2）过点B作BF⊥l于点F，连接BE，

∵AB为⊙O的直径，
∴∠AEB=90°，
又AD⊥l于点D，
∴∠AEB=∠ADF=∠BFD=90°，
∴四边形DEBF是矩形，
∴DE=BF．                         
∵AB为⊙O的直径，
∴∠ACB=90°，
∴∠ACD+∠BCF=90°．
∵∠ADC=90°，
∴∠ACD+∠CAD=90°，
∴∠BCF=∠CAD．
∵∠CAD=∠BAC，
∴∠BCF=∠BAC．                    
在Rt△BCF中，BC=6，
sin∠BCF=

BF

BC

=sin∠BAC=

3

5

，
∴BF=

3

5

BC=

18

5

，
∴DE=BF=

18

5

．

点评：本题考查了弦切角定理和圆周角定理、矩形的判定以及解直角三角形，作出辅助线构建等腰三角形、矩形是解题的关键．