题目内容
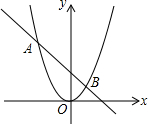 如图,抛物线y=ax2与直线y=bx+c的两个交点坐标分别为A(-2,4),B(1,1),则关于x的方程ax2-bx-c=0的解为
如图,抛物线y=ax2与直线y=bx+c的两个交点坐标分别为A(-2,4),B(1,1),则关于x的方程ax2-bx-c=0的解为考点:二次函数的性质
专题:数形结合
分析:根据二次函数图象与一次函数图象的交点问题得到方程组
的解为
,
,于是易得关于x的方程ax2-bx-c=0的解.
|
|
|
解答:解:∵抛物线y=ax2与直线y=bx+c的两个交点坐标分别为A(-2,4),B(1,1),
∴方程组
的解为
,
,
即关于x的方程ax2-bx-c=0的解为x1=-2,x2=1.
故答案为x1=-2,x2=1.
∴方程组
|
|
|
即关于x的方程ax2-bx-c=0的解为x1=-2,x2=1.
故答案为x1=-2,x2=1.
点评:本题考查了二次函数的性质:二次函数y=ax2+bx+c(a≠0)的顶点坐标是(-
,
),对称轴直线x=-
.也考查了二次函数图象与一次函数图象的交点问题.
| b |
| 2a |
| 4ac-b2 |
| 4a |
| b |
| 2a |

练习册系列答案
相关题目
关于圆有如下的命题:
①平分弦的直径垂直于弦;②不在同一条直线上的三点确定一个圆;③在一个圆中,90°的圆周角所对的弦是直径;④相等的圆心角所对的弧相等.
其中命题正确的是( )
①平分弦的直径垂直于弦;②不在同一条直线上的三点确定一个圆;③在一个圆中,90°的圆周角所对的弦是直径;④相等的圆心角所对的弧相等.
其中命题正确的是( )
| A、①② | B、②③ | C、③④ | D、①④ |
已知△ABC∽△DEF,相似比为1:2,△ABC的周长为4,则△DEF的周长为( )
| A、2 | B、4 | C、8 | D、16 |
在Rt△ABC中,∠C=90°,BC=3,AB=5,则cosB的值等于( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,大半圆的弦AB平行于直径CD,且与小半圆相切,已知AB=16cm,求图中阴影部分的面积.
如图,大半圆的弦AB平行于直径CD,且与小半圆相切,已知AB=16cm,求图中阴影部分的面积. 如图,∠AOB=90°,以O为顶点的锐角共有
如图,∠AOB=90°,以O为顶点的锐角共有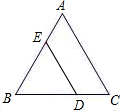 如图,△ABC是等边三角形,点D在BC边上,DE∥AC.求证:△BDE是等边三角形.
如图,△ABC是等边三角形,点D在BC边上,DE∥AC.求证:△BDE是等边三角形. (1)如图1,D是线段BC的中点,三角形ABC的面积与三角形ABD的面积比为
(1)如图1,D是线段BC的中点,三角形ABC的面积与三角形ABD的面积比为