题目内容
6.关于x的方程[mx2-(m-n)x-n](x2-6x+12)=0(其中m、n是实数,且m≠0)共有( )个不等实根.| A. | 2 | B. | 3 | C. | 4 | D. | 1或2 |
分析 解方程得x2-6x+12=0或mx2-(m-n)x-n=0,再结合两个方程的根的判别式的符号即可得出结论.
解答 解:若要[mx2-(m-n)x-n](x2-6x+12)=0,则需x2-6x+12=0或mx2-(m-n)x-n=0.
在方程x2-6x+12=0中,
△=b2-4ac=36-4×12=-12<0,
∴x2-6x+12=0无实数根;
在方程mx2-(m-n)x-n=0中,
∵m≠0,
∴△=b2-4ac=[-(m-n)]2-4m×(-n)=(m+n)2≥0,
∴方程mx2-(m-n)x-n=0有一个或两个实数根.
综上可知:关于x的方程[mx2-(m-n)x-n](x2-6x+12)=0(其中m、n是实数,且m≠0)共有一个或两个实数根.
故选D.
点评 本题考查了根的判别式,解题的关键是根据根的判别式的符号确定根的个数.本题属于基础题,难度不大,解决该题型题目时,由根的判别式的符号确定根的个数是关键.

练习册系列答案
相关题目
17.下列代数式运算正确的是( )
| A. | (x3)2=x5 | B. | x3•x2=x5 | C. | (2x)2=2x2 | D. | (x+2)2=x2+2 |
14.马大哈做题很快,但经常不仔细思考,所以往往错误率很高,有一次做了四个题,但只做对了一个,他做对的是( )
| A. | a8÷a4=a2 | B. | a3•a4=a12 | C. | $\sqrt{4}$=±2 | D. | 2x3•x2=2x5 |
1.下列计算正确的是( )
| A. | a2•a3=a6 | B. | (ab)2=a2b2 | C. | (a2)3=a5 | D. | a2+2a2=3a4 |
11. 如图,直线AB∥CD,∠C=115°,∠A=25°,则∠E的度数为( )
如图,直线AB∥CD,∠C=115°,∠A=25°,则∠E的度数为( )
 如图,直线AB∥CD,∠C=115°,∠A=25°,则∠E的度数为( )
如图,直线AB∥CD,∠C=115°,∠A=25°,则∠E的度数为( )| A. | 100° | B. | 90° | C. | 80° | D. | 70° |
18.已知点(-5,y1)、(-3,y2)都在直线y=-8x+7上,则y1、y2的大小关系为( )
| A. | y1>y2 | B. | y1=y2 | C. | y1<y2 | D. | 无法比较 |
15.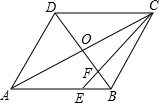 如图,在?ABCD中,AC与BD交于点O,E为AB上一点,且AE=2EB,连接CE交BD于点F,则S△BEF与S△COF的比值为( )
如图,在?ABCD中,AC与BD交于点O,E为AB上一点,且AE=2EB,连接CE交BD于点F,则S△BEF与S△COF的比值为( )
 如图,在?ABCD中,AC与BD交于点O,E为AB上一点,且AE=2EB,连接CE交BD于点F,则S△BEF与S△COF的比值为( )
如图,在?ABCD中,AC与BD交于点O,E为AB上一点,且AE=2EB,连接CE交BD于点F,则S△BEF与S△COF的比值为( )| A. | 1:3 | B. | 1:2 | C. | 2:3 | D. | 3:4 |
13.在下列调查中,适宜采用全面调查的是( )
| A. | 了解我省中学生视力情况 | |
| B. | 了解八(1)班学生校服的尺码情况 | |
| C. | 检测一批电灯泡的使用寿命 | |
| D. | 调查石家庄对《新闻联播》栏目的收视率 |