题目内容
15.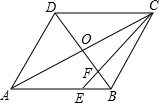 如图,在?ABCD中,AC与BD交于点O,E为AB上一点,且AE=2EB,连接CE交BD于点F,则S△BEF与S△COF的比值为( )
如图,在?ABCD中,AC与BD交于点O,E为AB上一点,且AE=2EB,连接CE交BD于点F,则S△BEF与S△COF的比值为( )| A. | 1:3 | B. | 1:2 | C. | 2:3 | D. | 3:4 |
分析 只要证明OF=FB,EF:CF=1:3即可解决问题.
解答  解:∵四边形ABCD是平行四边形,
解:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,OD=OB,
∵AE=2EB,
∴CD=3EB,
∴$\frac{EF}{FC}$=$\frac{BF}{DF}$=$\frac{EB}{DC}$=$\frac{1}{3}$,
∴OF=FB,
∴S△COF=S△BCF,S△EFB=$\frac{1}{3}$S△BCF,
∴S△EFB:S△BCF=1:3,
故选A.
点评 本题考查平行四边形的性质、平行线分线段成比例定理等知识,解题的关键是平行线分线段成比例定理的灵活运用,属于中考常考题型.

练习册系列答案
相关题目
3.下列命题是假命题的是( )
| A. | 若|a|=|b|,则a=b | |
| B. | 两直线平行,同位角相等 | |
| C. | 对顶角相等 | |
| D. | 若b2-4ac>0,则方程ax2+bx+c=0(a≠0)有两个不等的实数根 |
20.估计$\sqrt{3}$的值在( )
| A. | 1.4和1.5之间 | B. | 1.5和1.6之间 | C. | 1.6和1.7之间 | D. | 1.7和1.8之间 |
2.已知xa=3,xb=5,则x3a-2b=( )
| A. | 52 | B. | $\frac{3}{5}$ | C. | $\frac{9}{10}$ | D. | $\frac{27}{25}$ |
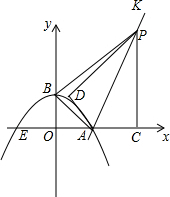 已知:如图,抛物线y=ax2+bx+2与x轴交于点A(4,0)、E(-2,0)两点,连结AB,过点A作直线AK⊥AB,动点P从A点出发以每秒$\sqrt{5}$个单位长度的速度沿射线AK运动,设运动时间为t秒,过点P作PC⊥x轴,垂足为C,把△ACP沿AP对折,使点C落在点D处.
已知:如图,抛物线y=ax2+bx+2与x轴交于点A(4,0)、E(-2,0)两点,连结AB,过点A作直线AK⊥AB,动点P从A点出发以每秒$\sqrt{5}$个单位长度的速度沿射线AK运动,设运动时间为t秒,过点P作PC⊥x轴,垂足为C,把△ACP沿AP对折,使点C落在点D处.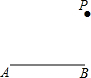 如图所示,已知:线段AB和点P.请用尺规按下列要求作图:①延长AB到C,使BC=2AB;②作射线BP;③连接PA,PC.
如图所示,已知:线段AB和点P.请用尺规按下列要求作图:①延长AB到C,使BC=2AB;②作射线BP;③连接PA,PC.