题目内容
20.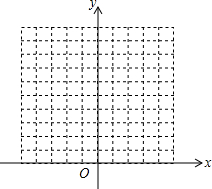 (1)用列表,描点的方法在同意直角坐标系中画出函数y=x+2和y=x2的图象
(1)用列表,描点的方法在同意直角坐标系中画出函数y=x+2和y=x2的图象(2)直接写出函数y=x+2和y=x2的交点坐标(-1,1)或(2,4)
(3)据图象当x+2>x2时,请直接写出x的范围-1<x<2
分析 (1)根据画函数图象的方法,先列表、再描点,然后再连线即可解答本题;
(2)根据函数图象可以直接写出函数y=x+2和y=x2的交点坐标;
(3)根据函数图象可以得到x+2>x2时的x的取值范围.
解答 解:(1)列表为:
作图为:
(2)由(1)中的函数图象可知函数y=x+2和y=x2的交点坐标是(-1,1)或(2,4).
故答案为:(-1,1)或(2,4);
(3)由(1)中的图象可知当x+2>x2时,x的取值范围是:-1<x<2.
故答案是:-1<x<2.
点评 本题考查二次函数和一次函数的图象,解题的关键是明确函数图象的画法,会画函数的图象,能根据函数图象回答问题.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
12.若二次函数y=-x2+2x+m2+1的最大值为4,则实数m的值为( )
| A. | $±\sqrt{2}$ | B. | $±\sqrt{3}$ | C. | ±2 | D. | ±1 |
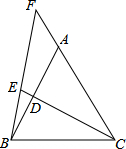 如图,△ABC为等边三角形,D为AB上一点,点E为CD延长线上一点,CE=CB,连接BE并延长交CA的延长线于点F,若AD=3,CF=7,则CD=4.
如图,△ABC为等边三角形,D为AB上一点,点E为CD延长线上一点,CE=CB,连接BE并延长交CA的延长线于点F,若AD=3,CF=7,则CD=4.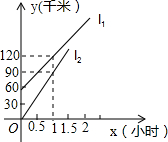 已知A,B地相距225千米,甲,乙两车都从A地出发,沿同一条高速公路前往B地,甲比乙早出发1小时,如图所示的l1,l2分别表示甲乙两车相对于出发地A的距离y(千米)与乙车行驶时间x(小时)之间的关系.根据图象提供的信息,解答下列问题:
已知A,B地相距225千米,甲,乙两车都从A地出发,沿同一条高速公路前往B地,甲比乙早出发1小时,如图所示的l1,l2分别表示甲乙两车相对于出发地A的距离y(千米)与乙车行驶时间x(小时)之间的关系.根据图象提供的信息,解答下列问题: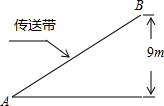 如图,传送带和地面所成的斜坡的坡度为1:$\sqrt{3}$,它把物体从地面送到离地面9米高的地方,则物体从A到B所经过的路程为18米.
如图,传送带和地面所成的斜坡的坡度为1:$\sqrt{3}$,它把物体从地面送到离地面9米高的地方,则物体从A到B所经过的路程为18米.