题目内容
5.已知二次函数y1=ax2+bx+c和一次函数y2=mx+n的图象交于两点A(-2,-5)和B(1,4),且二次函数图象与y轴的交点在直线y=2x+3上,求这两个函数的解析式.分析 先求出直线y=2x+3与y轴的交点,再把此交点坐标与A(-2,-5)和B(1,4)分别代入二次函数y1=ax2+bx+c,求出a、b、c的值即可得出其解析式;将A(-2,-5)和B(1,4)代入y2=mx+n求出m、n的值即可得出一次函数的解析式.
解答 解:∵y=2x+3与y轴交点为(0,3),
∴二次函数与y轴交点为(0,3),
将(0,3),A(-2,-5)和B(1,4)分别代入二次函数y1=ax2+bx+c得,
$\left\{\begin{array}{l}c=3\\ 4a-2b+c=5\\ a+b+c=4\end{array}\right.$,解得$\left\{\begin{array}{l}a=1\\ b=2\\ c=3\end{array}\right.$,
∴二次函数的解析式为:y1=x2+2x+3;
∵将A(-2,-5)和B(1,4)代入y2=mx+n得,-2m+n=-5,m+n=4,解得m=3,n=1,
∴一次函数y2=mx+n的解析式为:y2=3x+1.
点评 本题考查的是用待定系数法求二次函数的解析式,熟知二次函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
17.抛物线y=$\frac{1}{3}$x2,y=-3x2,y=-x2,y=2x2的图象开口最大的是( )
| A. | y=$\frac{1}{3}$x2 | B. | y=-3x2 | C. | y=-x2 | D. | y=2x2 |
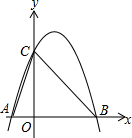 已知抛物线y=-x2+bx+c交x轴于点A(-1,0)和B(点A在B左侧),交y轴于点C,D点为抛物线顶点,若S△ABC=6,求抛物线解析式.
已知抛物线y=-x2+bx+c交x轴于点A(-1,0)和B(点A在B左侧),交y轴于点C,D点为抛物线顶点,若S△ABC=6,求抛物线解析式. (1)用列表,描点的方法在同意直角坐标系中画出函数y=x+2和y=x2的图象
(1)用列表,描点的方法在同意直角坐标系中画出函数y=x+2和y=x2的图象

 如果两个变量x、y之间的函数关系如图所示,则自变量x的取值范围是-3≤x≤3.
如果两个变量x、y之间的函数关系如图所示,则自变量x的取值范围是-3≤x≤3.