题目内容
9.画出下列反比例函数的图象:(1)y=$\frac{1}{2x}$;
(2)y=-$\frac{5}{x}$.
分析 (1)、(2)找出x、y的对应值列出表格,画出函数图象即可.
解答 解:(1)列表:
| x | -3 | -2 | -1 | 1 | 2 | 3 |
| y | $-\frac{1}{6}$ | $-\frac{1}{4}$ | $-\frac{1}{2}$ | $\frac{1}{2}$ | $\frac{1}{4}$ | $\frac{1}{6}$ |
 ;
;(2)
| x | -5 | -2 | -1 | 1 | 2 | 5 |
| y | 1 | $\frac{5}{2}$ | 5 | -5 | $-\frac{5}{2}$ | -1 |
 .
.点评 本题考查的是反比例函数的图象,熟知反比例函数的图象是双曲线是解答此题的关键.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
19.小莹用描点法画二次函数y=ax2+bx+c时,列出了下表:
(1)你能根据表格中的信息,求出该二次函数当x=3时,y的值吗?
(2)试从表中选择适当的数据,求出该二次函数的表达式.
| x | … | -2 | -1 | 0 | 1 | 2 | … |
| y | … | -$\frac{3}{16}$ | -4 | -$\frac{5}{2}$ | -2 | -$\frac{5}{2}$ | … |
(2)试从表中选择适当的数据,求出该二次函数的表达式.
17.抛物线y=$\frac{1}{3}$x2,y=-3x2,y=-x2,y=2x2的图象开口最大的是( )
| A. | y=$\frac{1}{3}$x2 | B. | y=-3x2 | C. | y=-x2 | D. | y=2x2 |
4.现在互联网越来越普及,网上购物的人也越来越多,订购的商品往往通过快递送达.淘宝网上某“四皇冠”级店铺率先与“快乐童年”童装厂取得联系,经营该厂家某种型号的童装.根据第一周的销售记录,该型号童装每天的售价x(元/件)与当日的销售量y(件)的相关数据如下表:
已知该型号童装每件的进价是70元,同时为吸引顾客,该店铺承诺,每件服装的快递费10元由卖家承担.
(1)请观察题中的表格,用所学过的一次函数、反比例函数或二次函数的有关知识,求第一周销售中,y与x的函数关系式;
(2)设第一周每天的赢利为w元,求w关于x的函数关系式,并求出每天的售价为多少元时,每天的赢利最大?最大赢利是多少?
(3)从第二周起,该店铺一直按第(2)中的最大日盈利的售价进行销售.但进入第三周后,网上其他购物店也陆续推出该型号童装,因此第三、四周该店铺每天的售价都比第二周下降了m%,销售量也比第二周下降了0.5m%(m<20);第五周开始,厂家给予该店铺优惠,每件的进价降低了16元;该店铺在维持第三、四周的销售价和销售量的基础上,同时决定每件童装的快递费由买家自付,这样,第五周的赢利相比第二周的赢利增加了2%,请估算整数m的值.
| 每件的销售价x(元/件) | 200 | 190 | 180 | 170 | 160 | 150 | 140 |
| 每天的销售量y(件) | 80 | 90 | 100 | 110 | 120 | 130 | 140 |
(1)请观察题中的表格,用所学过的一次函数、反比例函数或二次函数的有关知识,求第一周销售中,y与x的函数关系式;
(2)设第一周每天的赢利为w元,求w关于x的函数关系式,并求出每天的售价为多少元时,每天的赢利最大?最大赢利是多少?
(3)从第二周起,该店铺一直按第(2)中的最大日盈利的售价进行销售.但进入第三周后,网上其他购物店也陆续推出该型号童装,因此第三、四周该店铺每天的售价都比第二周下降了m%,销售量也比第二周下降了0.5m%(m<20);第五周开始,厂家给予该店铺优惠,每件的进价降低了16元;该店铺在维持第三、四周的销售价和销售量的基础上,同时决定每件童装的快递费由买家自付,这样,第五周的赢利相比第二周的赢利增加了2%,请估算整数m的值.
19.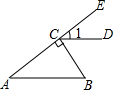 如图,BC⊥AE于点C,CD∥AB,∠1=35°,则∠B等于( )
如图,BC⊥AE于点C,CD∥AB,∠1=35°,则∠B等于( )
 如图,BC⊥AE于点C,CD∥AB,∠1=35°,则∠B等于( )
如图,BC⊥AE于点C,CD∥AB,∠1=35°,则∠B等于( )| A. | 35° | B. | 45° | C. | 55° | D. | 65° |
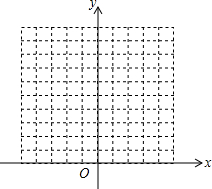 (1)用列表,描点的方法在同意直角坐标系中画出函数y=x+2和y=x2的图象
(1)用列表,描点的方法在同意直角坐标系中画出函数y=x+2和y=x2的图象
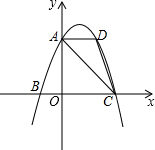 如图,已知二次函数y=ax2+bx+c(a≠0)的图象过A(0,3)、C(3,0)、D(2,3)三点.
如图,已知二次函数y=ax2+bx+c(a≠0)的图象过A(0,3)、C(3,0)、D(2,3)三点.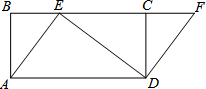 如图,四边形ABCD是矩形,点E在BC边上,点F在BC延长线上,且∠CDF=∠BAE.
如图,四边形ABCD是矩形,点E在BC边上,点F在BC延长线上,且∠CDF=∠BAE.