题目内容
9.若不等式组$\left\{\begin{array}{l}{6-3x≥0}\\{x-m≥0}\end{array}\right.$有实数解,则实数m的取值范围是m≤2.分析 根据大小小大中间找可得答案.
解答 解:由6-3x≥0,
解得x≤2.
由x-m≥0,解得x≥m,
由不等式组$\left\{\begin{array}{l}{6-3x≥0}\\{x-m≥0}\end{array}\right.$有实数解,则实数m的取值范围是m≤2,
故答案为:m≤2.
点评 此题主要考查了一元一次不等式组解集的求法,其简便求法就是用口诀求解.求不等式组解集的口诀:同大取大,同小取小,大小小大中间找,大大小小找不到(无解).

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
8.一元二次方程x2+2x+1=0的根的情况是( )
| A. | 有两个相等的实数根 | B. | 有两个不相等的实数根 | ||
| C. | 没有实数根 | D. | 只有一个实数根 |
14. 有这样一个问题:探究函数y=$\frac{1}{2}$(x-1)(x-2)(x-3)+x的性质.
有这样一个问题:探究函数y=$\frac{1}{2}$(x-1)(x-2)(x-3)+x的性质.
(1)先从简单情况开始探究:
①当函数y=$\frac{1}{2}$(x-1)+x时,y随x增大而增大(填“增大”或“减小”);
②当函数y=$\frac{1}{2}$(x-1)(x-2)+x时,它的图象与直线y=x的交点坐标为(1,1),(2,2);
(2)当函数y=$\frac{1}{2}$(x-1)(x-2)(x-3)+x时,
下表为其y与x的几组对应值.
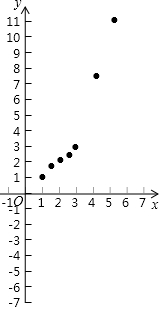
①如图,在平面直角坐标系xOy中,描出了上表中各对对应值为坐标的点,请根据描出的点,画出该函数的图象;
②根据画出的函数图象,写出该函数的一条性质:y随x的增大而增大.
 有这样一个问题:探究函数y=$\frac{1}{2}$(x-1)(x-2)(x-3)+x的性质.
有这样一个问题:探究函数y=$\frac{1}{2}$(x-1)(x-2)(x-3)+x的性质.(1)先从简单情况开始探究:
①当函数y=$\frac{1}{2}$(x-1)+x时,y随x增大而增大(填“增大”或“减小”);
②当函数y=$\frac{1}{2}$(x-1)(x-2)+x时,它的图象与直线y=x的交点坐标为(1,1),(2,2);
(2)当函数y=$\frac{1}{2}$(x-1)(x-2)(x-3)+x时,
下表为其y与x的几组对应值.
| x | … | -$\frac{1}{2}$ | 0 | 1 | $\frac{3}{2}$ | 2 | $\frac{5}{2}$ | 3 | 4 | $\frac{9}{2}$ | … |
| y | … | -$\frac{113}{16}$ | -3 | 1 | $\frac{27}{16}$ | 2 | $\frac{37}{16}$ | 3 | 7 | $\frac{177}{16}$ | … |
②根据画出的函数图象,写出该函数的一条性质:y随x的增大而增大.
19.对于等式:(1)(-am)n=(-an)m;(2)[(-a)m]n=[(-a)n]m.判断正确的是( )
| A. | (1)正确 | B. | (2)正确 | C. | 都正确 | D. | 无法判断 |